Question

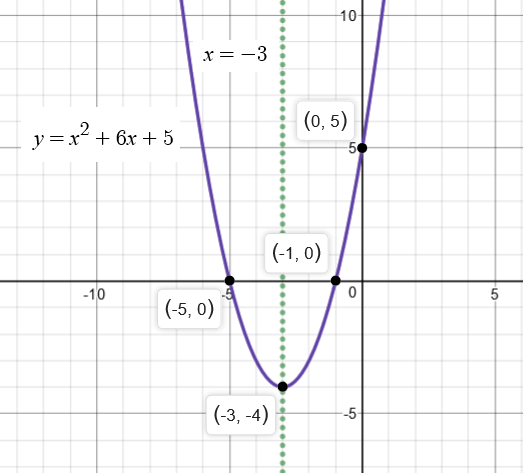
How do find the vertex and axis of symmetry, and intercepts for a quadratic equation `y= x^2 + 6x + 5`?

Answer 1

Vertex : `color(blue)((-3, -4)`

Axis of Symmetry is at : `color(blue)(x=(-3)`

x-intercepts: `color(blue)((-1,0) and (-5,0)`

y-intercept: `color(blue)((0,5)`

Explanation:

Given:

`color(red)(y = f(x) = x^2+6x+5`

The Vertex Form of a quadratic function is given by:

`color(blue)(f(x)=a(x-h)^2+k`, where `color(green)((h,k)` is the Vertex of the parabola.

`color(green)(x=h` is the axis of symmetry.

Use completing the square method to convert `color(red)(f(x)` into Vertex Form.

`color(red)(y = f(x) = x^2+6x+5`

Standard Form `rArr ax^2+bx+c=0`

Consider the quadratic `x^2+6x+5=0`

`color(blue)(a=1; b=6 and c=5`

Step 1 - Move the constant value to the right-hand side.

Subtract 5 from both sides.

`x^2+6x+5-5 = 0-5`

`x^2+6x+cancel 5-cancel5 = 0-5`

`x^2+6x=-5`

Step 2 - Add a value to both sides.

What value to add?

Add the square of `b/2`

Hence,

`x^2+6x+[(6/2)^2]=-5+[(6/2)^2]`

`x^2+6x+9=-5+9`

`x^2+6x+9=4`

Step 3 - Write as Perfect Square.

`(x+3)^2=4`

Subtract `4` from both sides to get the vertex form.

`(x+3)^2-4=cancel 4-cancel 4`

`f(x)=(x+3)^2 - 4`

Now, we have the vertex form.

`color(blue)(f(x)=a(x-h)^2+k`, where `color(green)((h,k)` is the Vertex of the parabola.

Hence, Vertex is at `color(blue)((-3,-4)`

Axis of Symmetry is at `color(red)(x=h`

Note that `h=-3`

`rArr color(blue)(x= -3`

Step 4 - Write the x, y intercepts.

Consider

`(x+3)^2=4`

To find the solutions, take square root on both sides.

`sqrt((x+3)^2)= +-sqrt(4)`

`rArr x+3=+-2`

There are two solutions.

`x+3 = 2`

`rArr x=2-3 = -1`

Hence, `x=-1` is one solution.

Next,

`x+3=-2`

`x=-2-3=-5`

Hence, `x=-5` is the other solution.

Hence, we have two x-intercepts: `(-1,0) and (-5,0)`

To find the y-intercept:

Let `x=0`

We have,

`f(x)=(x+3)^2 - 4`

`f(0)=(0+3)^2-4`

`rArr 3^2-4 = 9-4 = 5`

Hence, y-intercept is at `y=5`

`rArr color(blue)((0,5)`

Analyze the image of the graph below: