How do I find the determinant of a matrix using Gaussian elimination?
1 Answer
A determinant of a square matrix is different from Gaussian elimination...so I will address both topics lightly for you!
The determinant of a 2x2 matrix 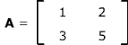 is found by subtracting the products of the diagonals like:
is found by subtracting the products of the diagonals like:
For a larger square matrix like a 3x3, there are different methods. Link to Purple math for one method.
The TI-nspire calculator (as well as other calculators and online services) can do a determinant quickly for you: 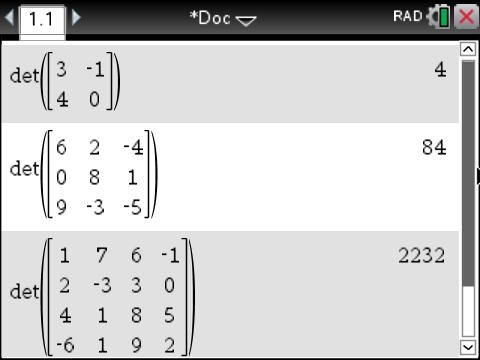
Gaussian elimination is a method of solving a system of linear equations. First, the system is written in "augmented" matrix form. Then, legal row operations are used to transform the matrix into a specific form that leads the student to answers for the variables.
Ex: 3x + 4y = 10
-x + 5y = 3
The command "ref" on the TI-nspire means "row echelon form", which takes the matrix down to a stage where the last variable is solved for, and the first coefficient is "1".

In this example, y = 1, and
Without showing you all of the steps (row operations), you probably don't have the feel for how to do this yourself! Here is another LINK to Purple Math to see what they say about Gaussian elimination.

