How do I solve the rational inequality #(x+2)/(2x+1)>5# using a TI-84?
1 Answer
Jul 20, 2017
# -1/2 lt x lt -1/3 #
Explanation:
On a TI-nspire CAS we can evaluate algebraic expressions directly:
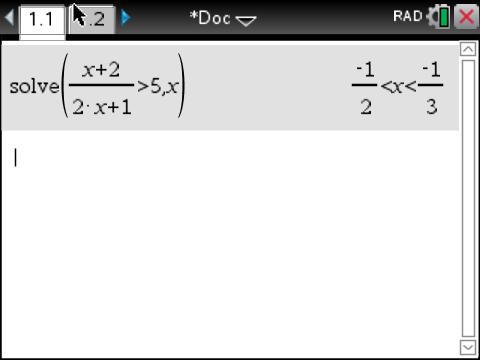
Otherwise we can solve the equation to get the critical points:
# (x+2)/(2x+1) = 5 #
# :. (x+2)/(2x+1) - 5 = 0 #
# :. ((x+2) - 5(2x+1))/(2x+1) = 0 #
# :. (x+2 - 10x-5)/(2x+1) = 0 #
# :. (3x+1)/(2x+1) = 0 #
So the critical points (where a sign change can occur) are:
# 3x+1 => x=-1/3 #
# 2x+1 = 0 => x=-1/2#
Then using a graphic calculator:
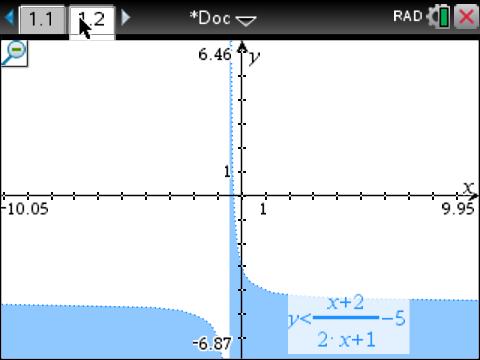
We conclude the same result as above.

