If #f# is a function which maps #x# to #y#, then #f^(-1)# is a function that maps #y# to #x#. However, if #f(x)# maps more than one #x# value to a single #y#, then there is no way to know which #x# #f^(-1)# should map #y# to.
If you don't care about about the inverse being a function, then we can just consider all the cases, similar to how we invert #y=x^2# by swapping #y# and #x# and then solving for #y#: #x = y^2 => y = +-sqrt(x)#. Doing so for #f(x) = |2-x|#, we get
#x = |2-y|#
#=> x = +-(2-y)#
#=> +-x = 2-y#
#=> y = 2+-x#
So the inverse is #y = 2+-x#. Note that as #f(x)>=0# in the initial function, we must have #x>=0# for the inverse. This gives us the graph
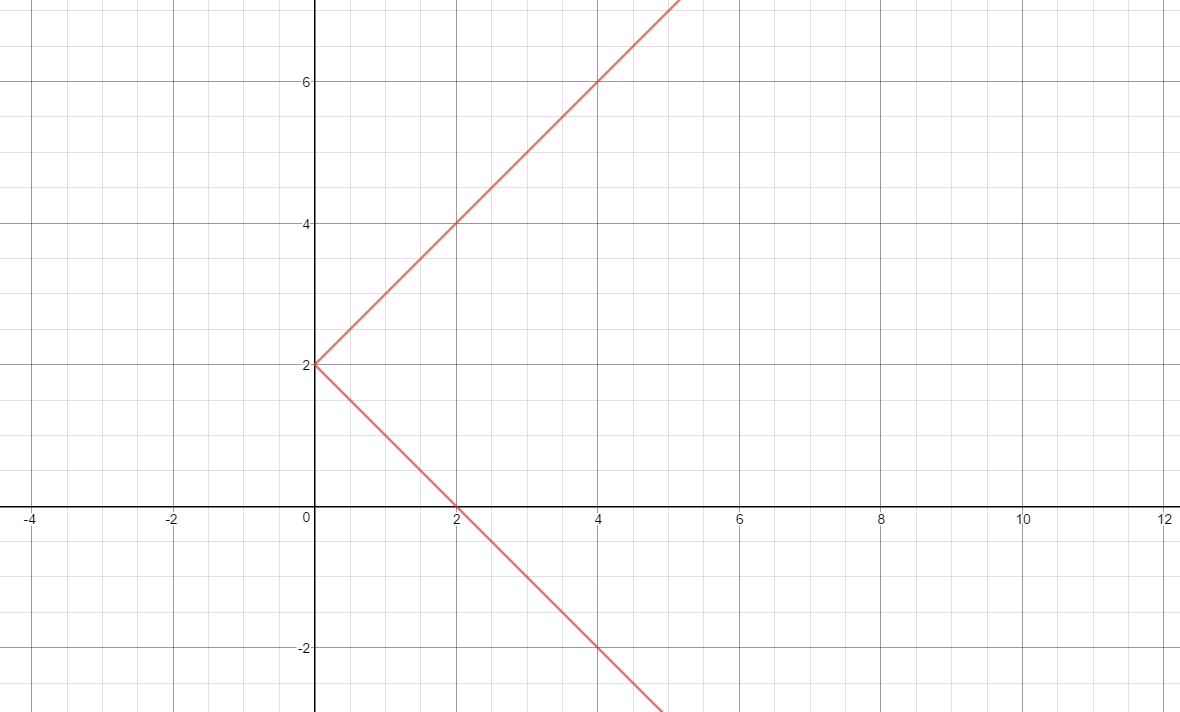
which is a reflection of #y = |2-x|# across the line #y=x#, as we would expect .
If we want to have the inverse as a function, then we must consider a restriction of #|x-2|# to a domain in which every #x# value is mapped to a distinct #y# value (a function with this property is called one-to-one).
Again, this is analogous to finding the inverse of #g(x)=x^2#. If we add the initial restriction #x <= 0#, then we get #x = -sqrt(x^2) => g^(-1)(x) = -sqrt(x)#. If we add the initial restriction #x>=0#, then we get #x = sqrt(x^2) => g^(-1)(x) = sqrt(x)#. Notice that we get a different inverse function depending on how we restrict the domain of #g(x)#.
Because #f(x)# is defined as
#f(x) = {(-(x-2) if x-2 <= 0), (x-2 if x-2>=0):}#
#=> f(x) = {(2-x if x <= 2), (x-2 if x>=2):}#
natural restrictions would be considering #f(x) = |2-x|, x<=2# or #f(x) = |2-x|, x>=2#. Then we are just finding the inverse of #2-x# or #x-2# on the restricted interval.


