How do you combine #(5x+2)/(x-4) + (x+3)/(x+1)#?
2 Answers
May 20, 2015
Try this:
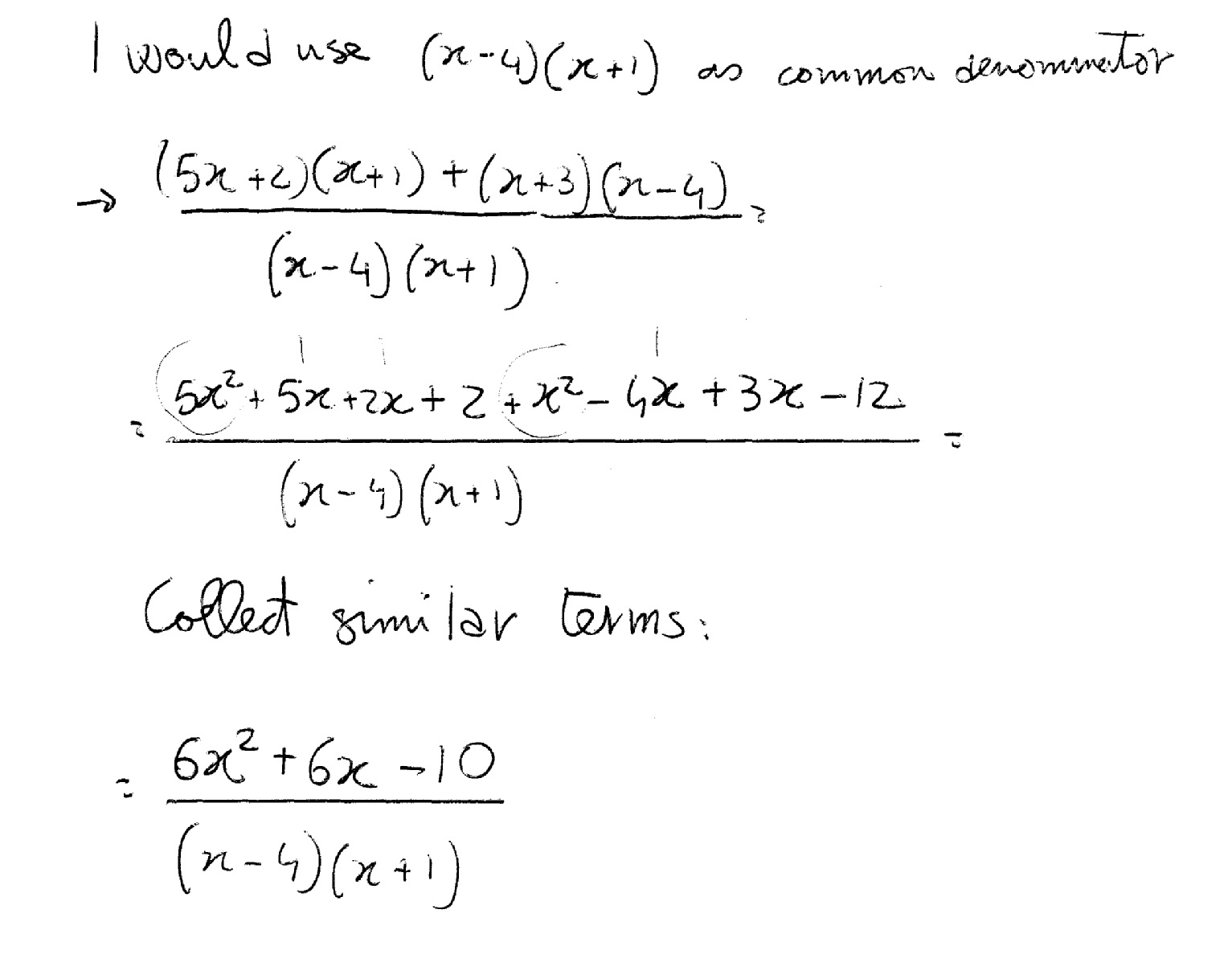
May 21, 2015
The answer is
Sorry, this is a long answer.
Problem: Combine
Multiply the numerator and denominator of
Multiply the numerator and denominator of
We now have common denominators. Combine terms.
Group like terms.
Simplify.
Factor out the GCF


