How do you convert # (1, (3pi )/ 4) # into cartesian form?
1 Answer
Oct 25, 2016
Explanation:
An angle of
Here is a fairly standard image of this relationship
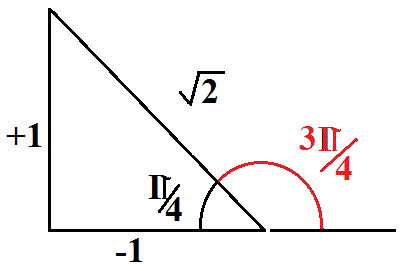
However the polar coordinates tell us that the radius (hypotenuse) needs to be
so all sides need to be scaled down by dividing by
giving x-coordinate:
