How do you convert #(-2,0)# from cartesian to polar coordinates?
1 Answer
Polar form:
Explanation:
Given:
Cartesian coordinates:
How do we convert from Cartesian coordinates to Polar form?
Polar Form:
Examine the sketch below:
Important formula to remember:
Let us identify the point on the Cartesian Plane:
Cartesian coordinates:
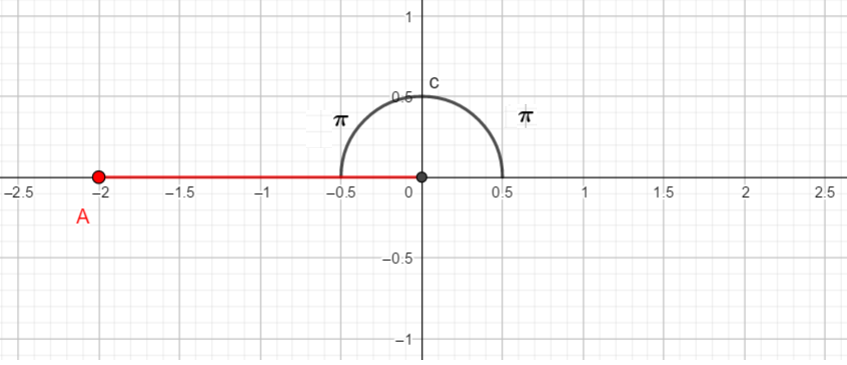
Note that the angle is
Hence
Use the formula:
Swap sides:
Taking the
Hence, the required Polar form:
Hope this helps.

