Question

How do you convert `2=(2x+3y)^2-x` into polar form?

Answer 1

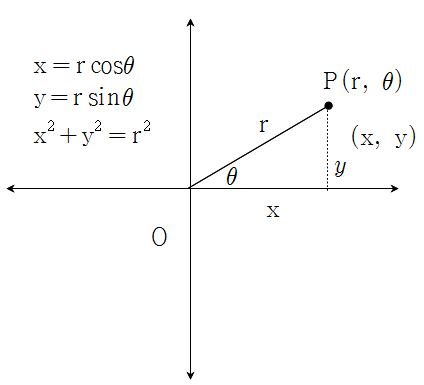
In the diagram above, we can see the relation between the rectangular and polar coordinates of a given point in the plane.

Thus, `2=(2x+3y)^2-x` in polar form is going to be

`2=(2rcostheta+3rsintheta)^2-rcostheta`

Which, after some simplifications, becomes

`2=r^2(4+5sin^2theta+3sin2theta)-rcostheta`

If you want, you can go the extra mile and solve the quadratic equation with undeterminate `r` to write `r` as a function of `theta`.