How do you convert #(-4,-4)# into polar form?
1 Answer
Explanation:
To convert between polar and rectangular, these formulas will help you out. (Link to the webpage I got the image from is in gray.)
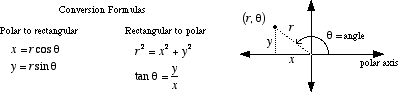
So we can see that where the Cartesian/rectangular ordered pairs follow the
The steps here can vary, depending on whether you want to find
We should note, however, that since
We can use one of the left-hand formulas to find
So we have found our answer:
Of course, the way you write your answer is going to depend on whether they want

