How do you convert #r^2 = 9cos5(theta)# into cartesian form?
1 Answer
Explanation:
Here,
And so,
The period for the graph is
For one half (
Only for half period =
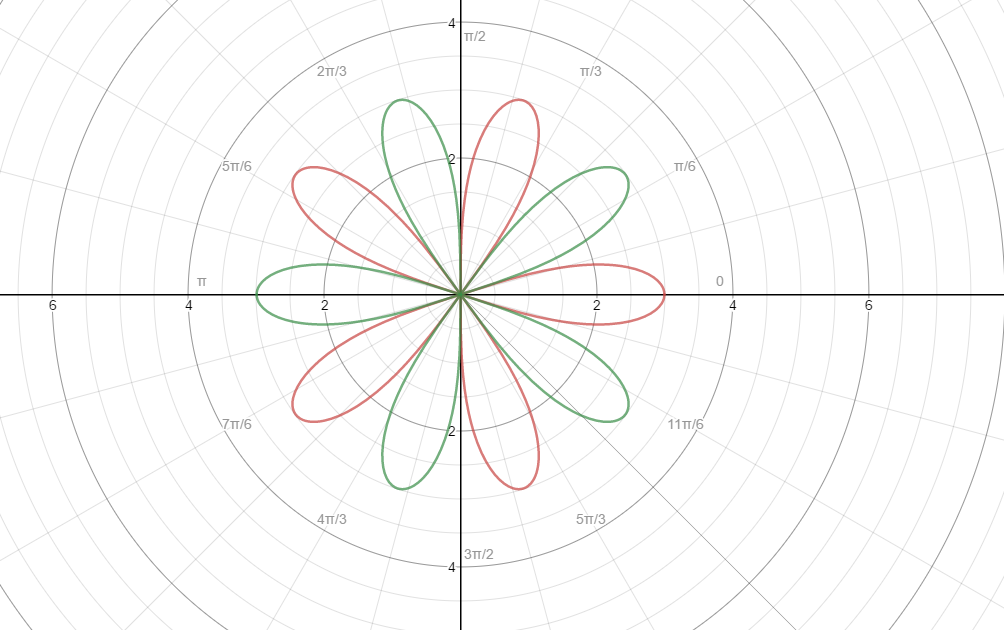
I expect five equal loops like the ones that are marked red in the
second graph, contributed by the other author.
The conversion formula is
Substitution gives the form in the answer.
graph{(x^2+y^2)^3.5-9x^5+90x^3y^2-45xy^4=0}
Debugging was elusive for me, for so long. I was able to do it now.
Adikesavan's revised answer ends here.
Here is a graph where the red is the positive value for r and the green is the negative values for r: