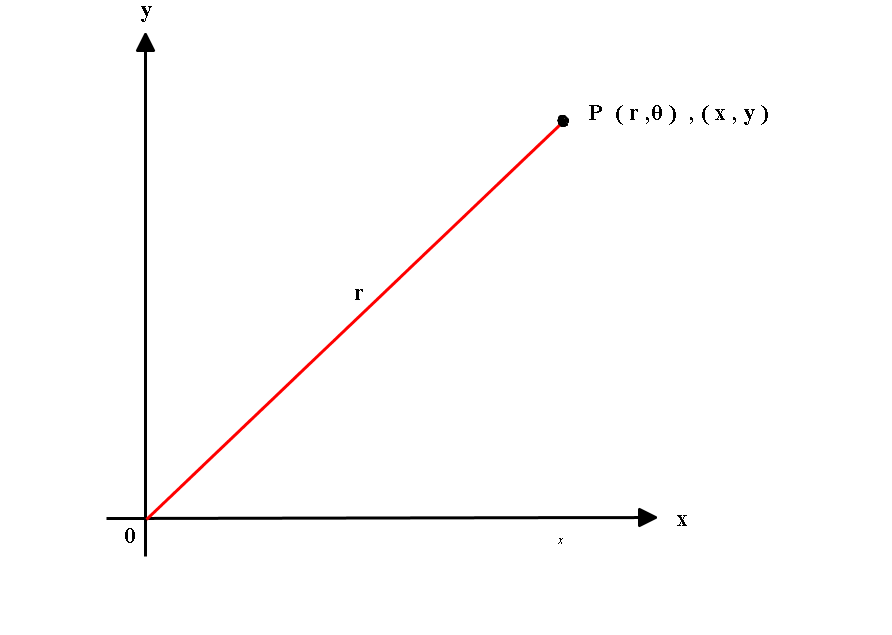
From the diagram we can see that point P has polar coordinates
#( r , theta )# and Cartesian coordinates #(x,y)#.
And #color(white)(88)x=rcos(theta)# , #y = rsin(theta)#
#(x,y) -> (rcos(theta), rsin(theta))#
Also:
By Pythagoras' Theorem :
#r^2=(rcostheta)^2+(rsintheta)^2#
Since:
#x=rcos(theta)# and #y = rsin(theta)#
Then:
#r^2=x^2+y^2# #:. r=sqrt(x^2+y^2)#
Using these ideas:
#r=4/(1-cos(theta))#
Substituting:
#sqrt(x^2+y^2)=4/(1-cos(theta))#
#cos(theta)=x/r#
#sqrt(x^2+y^2)=4/(1-x/r)#
#sqrt(x^2+y^2)=4/(1-x/(sqrt(x^2+y^2))#
Multiply by #(1-x/(sqrt(x^2+y^2)))#
#sqrt(x^2+y^2)-(xsqrt(x^2+y^2))/(sqrt(x^2+y^2))=(4(1-x/(sqrt(x^2+y^2))))/(1-x/(sqrt(x^2+y^2))#
#sqrt(x^2+y^2)-(xcancel(sqrt(x^2+y^2)))/(cancel(sqrt(x^2+y^2)))=(4(cancel(1-x/(sqrt(x^2+y^2)))))/((cancel(1-x/((sqrt(x^2+y^2))))))#
#sqrt(x^2+y^2)-x=4#
#sqrt(x^2+y^2)=4+x#
Squaring:
#x^2+y^2=x^2+8x+16#
#y^2-8x-16=0#


