How do you convert r=6sectheta into cartesian form?
1 Answer
Jul 13, 2016
Explanation:
To convert from polar to cartesian, we can make use the following:
Since
We can simplify this expression even further since
So our final answer is
We can check this by graphing, for example.
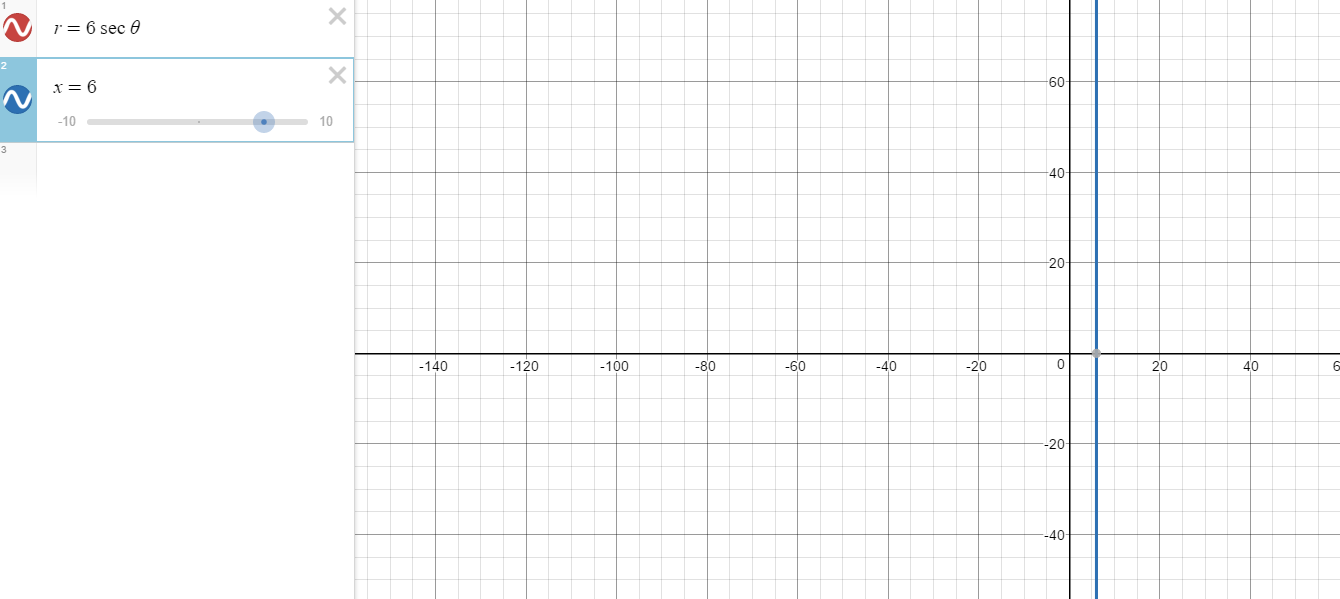
In this graph,

