How do you convert #rcos(t) = 4# into a rectangular equation?

Question

3990 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-07-13T20:53:27

#x=4#

Consider a point #P# with rectangular coordinates #(x,y)# and polar coordinates #(r,theta)#:

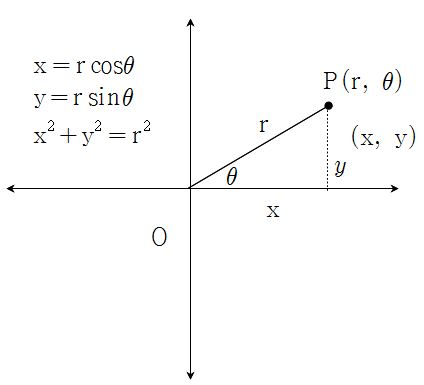
As we can see in the diagram above, we can state some relations between the rectangular and polar coordinates:

#costheta = x/r => x=rcostheta#

#sintheta=y/r => x=rsintheta#

#x^2+y^2=r^2#

It is worth to note that the name of the angle variable does not matter; calling it #t# is equivalent to calling it #theta#. As such, the function

#rcost=4#

is equivalent to saying

#x=4#

in rectangular form.