How do you determine circle, parabola, ellipse, or hyperbola from equation #x^2 + y^2 - 16x + 18y - 11 = 0#?

Question

9707 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-11-30T12:45:24

The equation is of a circle of radius #sqrt(156)# centered at #(8, -9)#

Step 1: Group #x#'s and #y#'s

#x^2 - 16x + y^2 + 18y = 11#

Step 2: Complete the square for both #x# and #y#

#x^2 - 16x + 64 + y^2 + 18y + 81 = 11 + 64 + 81#

#=>(x - 8)^2 + (y + 9)^2 = 156#

Step 3: Compare to the standard forms of conic sections

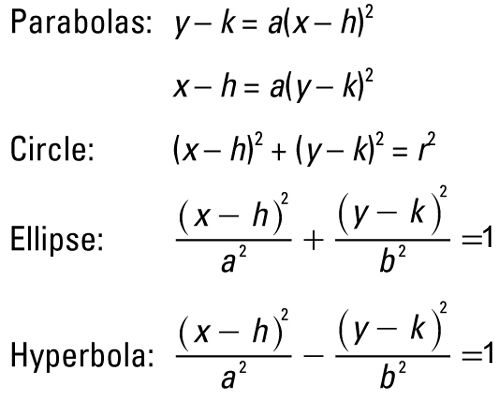
Note that the above equation matches the formula for a circle with #h = 8#, #k = -9#, and #r = sqrt(156)#

Thus the equation is of a circle of radius #sqrt(156)# centered at #(8, -9)#