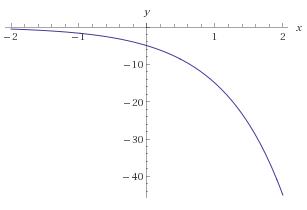
How do you determine if the equation # y = -5(1/3) ^ -x# represents exponential growth or decay?
1 Answer
May 2, 2016
Let us define what is an exponential function, and when it grows or decays.
Explanation:
An exponential function is any function in the form:
where
Now, there are two type of exponential behaviours:
- Exponential growth: the value of
#y(x)# tends to#infty# when#x to infty# . - Exponential decay: the inverse to exponential growth.
Note: we shall note that
Let us distinguish several cases, according to this:
- If
#b > 1# , multiplying#b# many times will increase its value. However, if exponent#cx# is negative (because#c <0# ), then we will have something like
#b^{-x} ~ 1/b^x#
and this does not grow, but degrows when#x to infty# . - The inverse happens when
#b < 1# : it grows if#c > 0# , and degrows if#c < 0# . In this case, multiplying#b# many times decreases its final value:
#1/2 cdot 1/2 = 1/4 " , " 1/2 cdot 1/2 cdot 1/2 = 1/8 < 1/4 ...# - These explanations are right if
#a > 0# . If#a<0# , then the results are the opposites.
So, to sum up:
- If
#b > 1# , then:
#color(blue) ((1))# If#a,c# are both possitive or negative, we find exponential growth.
#color(blue) ((2))# If#a,c# have different signs, we find exponential decay. - If
#b < 1# , then:
#color(blue) ((3))# If#a, c# are both possitive or negative, we find exponential decay.
#color(blue) ((4))# If#a, c# have different sign, we find exponential growth.
On this link you cand find an example of each case.
So, finally,