Exponential Decay

Key Questions

  • How do you determine if an exponential formula is growth or decay?

    #f(t)=Ce^{kt}# is an exponential #{("growth if " k>0),("decay if " k<0):}#.

    I hope that this was helpful.

    Wataru · 1 · Nov 12 2014
  • How do you graph exponential decay functions?

    This is an example for the function #f(x)=2*e^(-3 x)#

    This is just a particular case of the general form #f(x)=a*e^(k x)#
    where #a# is a constant representing the value at start and #k# is the rate of growth (when #k>0#) or the rate of decay (when #k<0#).

    (Please note that #f# is always a function of time, so the symbol #t# it is often used instead of #x#).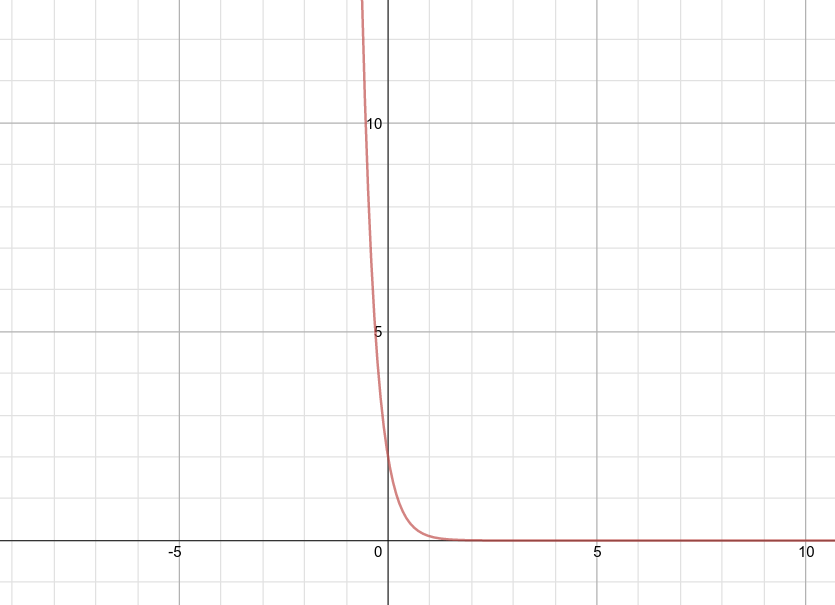

    enter image source here

    Alex Boroda · 1 · May 21 2015
  • What is the exponential decay formula?

    It's of the form #N=B*g^t# where #g<1#

    N = current (new) situation
    B = beginning situation (start-value)
    g = growth factor
    t = number of time periods, this may be hours, days, whatever

    Growth factor is what you multiply the value of one period with in order to get the value for the next. If the growth factor is less than 1, we speak of decay, because every next period will give a lesser value.

    Let's take an example. The radio-activity of a certain object starts at 1000 units and gets less by 10% every week. What can we expect after 10 weeks?
    First we determine the growth factor: 10% off means 90%, or 900 left after one week, 90% of 900, or 810 left after the second week and so on. The 'growth' factor is thus 0.9, because the startvalue, and all values after that, are multiplied by 0.9 to get to the next value.
    In this case the formula would be: #N=1000*0.9^t#
    with #t# in weeks.
    After 10 weeks this would lead to #N=1000*0.9^10=348.68# (rounded)

    Watch it! In exams they often switch between units. A question may be: 'What is the radio-activity after one year' -- of course you then would use #g^52#, wouldn't you?

    MeneerNask · 1 · Dec 23 2014

Questions

Exponents and Exponential Functions