Question

How do you determine the values of the coefficients a and b that will give a minimum value of the area, `S`, of the region enclosed by the curve `y=-x^2+ax+b` (which passes through point (1,2)) and the curve `y=(1/2)x^2`?

Answer 1

`S=2`

Explanation:

Calling

`f_1(x)=-x^2+ax+b`
`f_2(x)=1/2x^2`

the intersection points between `f_1` and `f_2` are obtained solving

`{(f_1(1)=2->-1+a+b=2),(f_1(x)=y->-x^2+ax+b=y),(f_2(x)=y->1/x^2=y):}`

Solving for `x,y,a` we obtain

#((x = 1/3 (3 - b - sqrt[9 + b^2]), y = 1/9 (9 - 3 sqrt[9 + b^2] + b (-3 + b + sqrt[9 + b^2]))), (x = 1/3 (3 - b + sqrt[9 + b^2]), y = 1/9 (b^2 + 3 (3 + sqrt[9 + b^2]) - b (3 + sqrt[9 + b^2]))))#

with `a=3-b`

so the intersection points are at

`x_i=1/3 (3 - b - sqrt[9 + b^2])`
`x_s=1/3 (3 - b + sqrt[9 + b^2])`

The enclosed area is

`S(b)=int_(x=x_i)^(x=x_s)(f_1(x)-f_2(x))dx = 1/2 (x_i - x_s) (-2 b + x_i^2 + x_i x_s + x_s^2 - (3-b)(x_i + x_s))`

Substituting now `x_i` and `x_s` we obtain

`S(b)=2/27 (9 + b^2)^(3/2)` with a minimum at `b=0`

So finally `a=3,b=0` and `S=2`

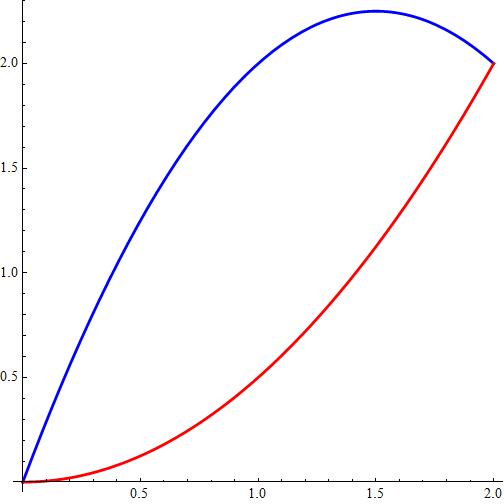
Attached a plot showing `f_1(x)` blue and `f_2(x)` red.