How do you differentiate #(x-1)/sqrt(6-x)#?
1 Answer
By using quotient rule:
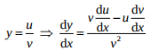
Explanation:
Let
Plugging this into the formula, you get:
Step one:
Step two: simplify
Step three: split numerator
Step Four: combine the
Step Five: write with positive exponents only
There may be other ways to further simplify the derivative, but this is what I would have done.
For future questions like this, use https://www.derivative-calculator.net/ It gives you the step by step process for any differentiation.

