How do you divide (x^2+12x+16) / (x+4)?
2 Answers
(x+8)
Explanation:
Use long division.
Long division with polynomials is hard to explain in words, so I attached a picture that goes along with the steps. Hopefully it's clear to understand.
Steps of long division with polynomials:
1. First term of dividend polynomial (the one inside the division box) divided by the first term of the divisor (outside of box), this is the first term of the quotient.
2. Multiply the divisor polynomial by the first term of the quotient to get another polynomial and subtract this polynomial from the dividend.
3. Bring down the next term in the dividend.
4. Repeat steps 1-3, but with the first term of the newly subtracted dividend to get the second term of the quotient and so on.
5. At some point you will reach a number in the dividend that has no variable, but it's just a number. This is your remainder (R). The way you write a remainder in the quotient is R divided by the divisor. So in this case, R=-16, so the remainder in the quotient is -16/(x+4)
This depicts the steps as best as I could:
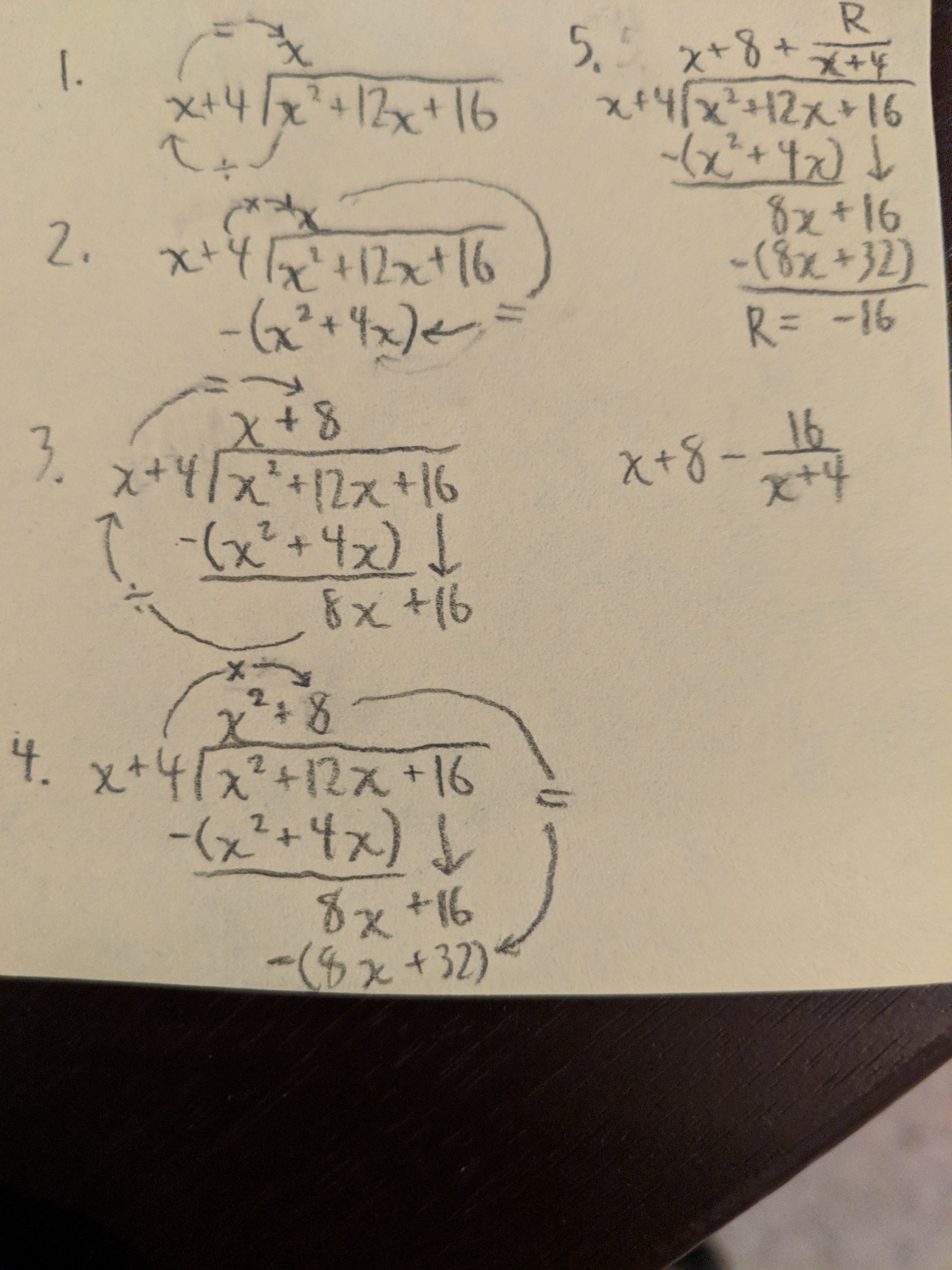
Explanation:


