Question

How do you divide `(x^3 + x^2 - x - 1)/(x - 1)` using polynomial long division?

Answer 1

Long division of polynomials is similar to long division of numbers.

See explanation...

Explanation:

Here's an animation of the process:

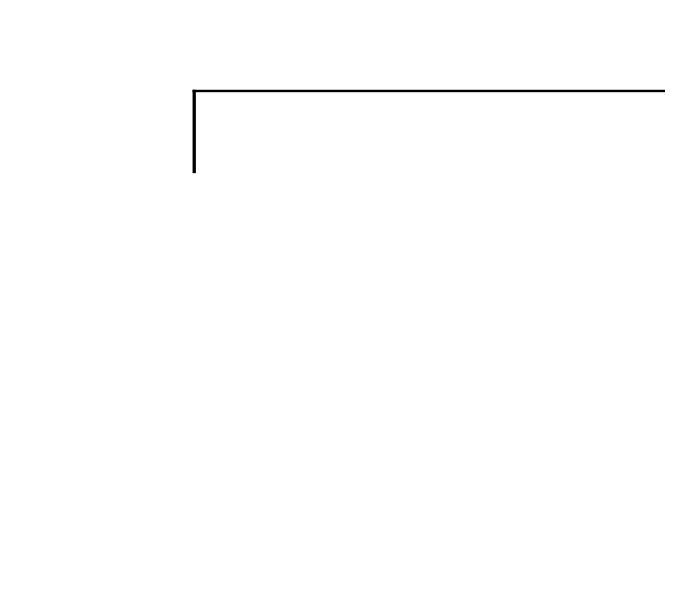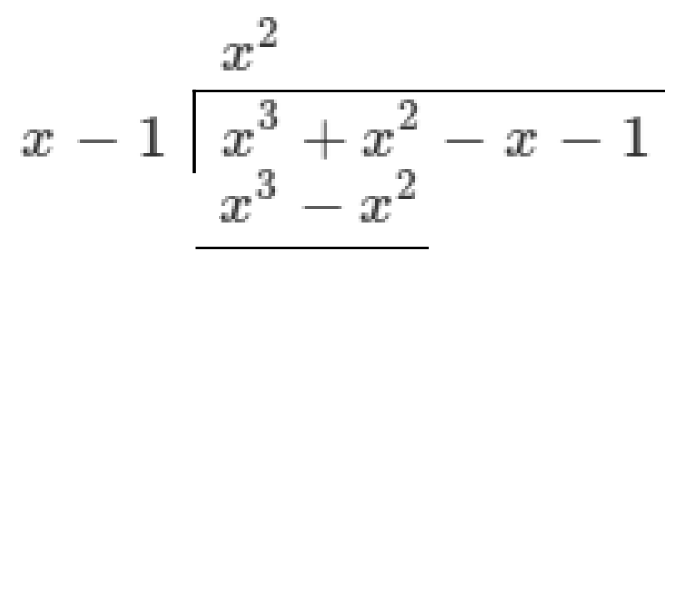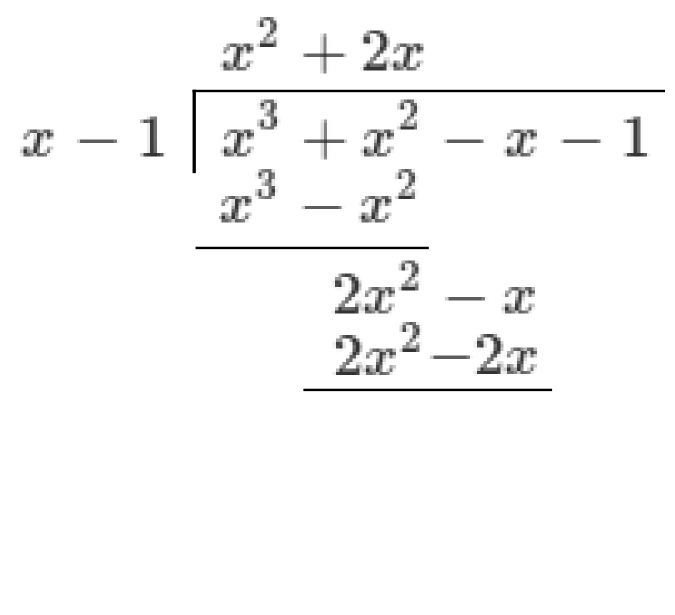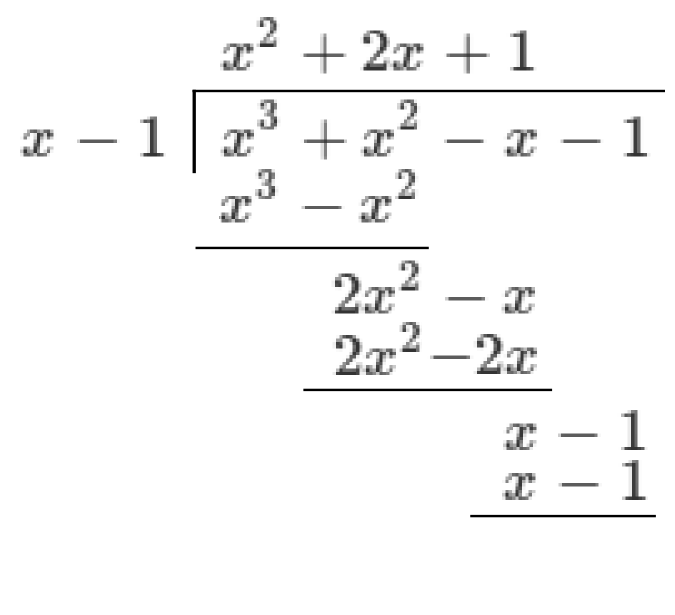
Write the dividend under the bar and the divisor to the left. Each is written in descending order of powers of `x`. If any power of `x` is missing, then include it with a `0` coefficient. For example, if you were dividing by `x^2-1`, then you would express the divisor as `x^2+0x-1`.

Choose the first term of the quotient to cause leading terms to match. In our example, we choose `x^2`, since `(x-1)*x^2 = x^3-x^2` matches the leading `x^3` term of the dividend.

Write the product of this term and the divisor below the dividend and subtract to give a remainder (`2x^2`).

Bring down the next term (`-x`) from the divisor alongside it.

Choose the next term (`2x`) of the quotient to match the leading term of this remainder, etc.

Stop when there is nothing more to bring down from the dividend and the running remainder has lower degree than the divisor.

In our example, the division is exact. We are left with no remainder.