You need to understand the base sine graph, and how to do basic transformations.
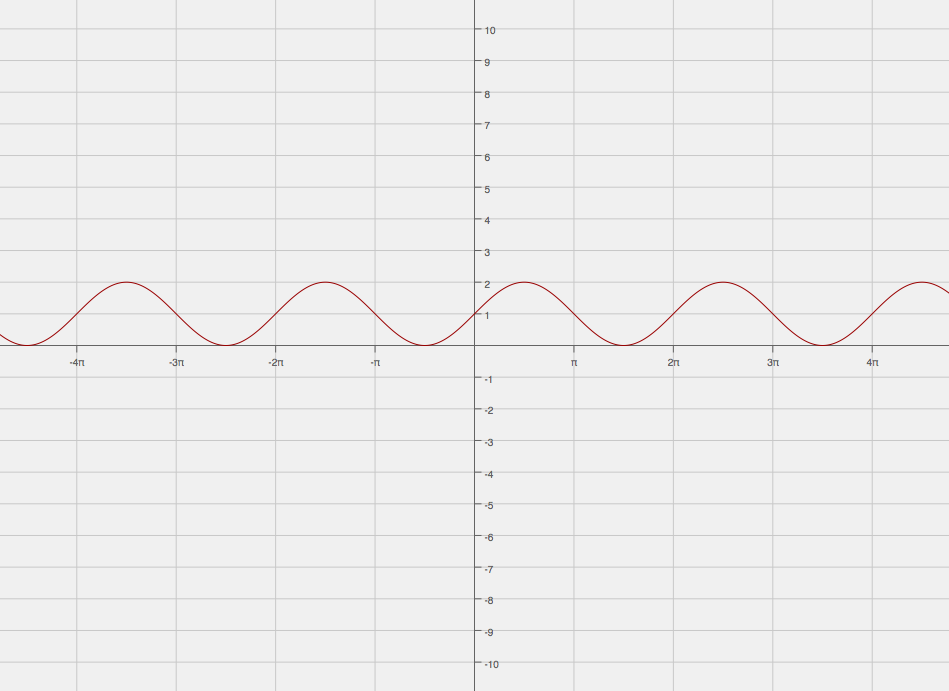
The graph of #sinx# will have its #y#-intercept at #x = 0#. It has an amplitude of #1#, so it will always have a maximum of #y= 1# and a minimum of #y = -1#. It first goes up, and then comes back down to reach a minimum, passing through the line #y= 0#, which is in fact the axis of symmetry.
The period of sine is #2pi#, that's to say it takes #2pi# units for it to repeat itself.
As for #y = 1 + sinx#, this is the graph of #y = sinx#, with the axis of symmetry moved up #1# unit to #y = 1#. The graph of #y = 1 + sinx# is shown in the following image.
Hopefully this helps!


