How do you evaluate sine, cosine, tangent of #pi/4# without using a calculator?
2 Answers
Explanation:
Hence
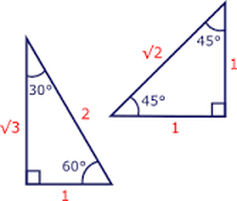
Now, you can find the sine, cosine and tangent without a calculator!
You should obtain
Sin and cosine:
Tangent:
I am assuming you are familiar with the formula SOH CAH TOA, yes?
Start by drawing a right triangle in Quadrant I, with a
Explanation:
The
I teach that
Take the square root of both sides:
If each side =


