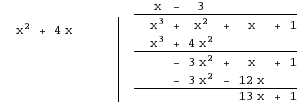We start by dividing #x^3 + x^2 + x + 1# by #x^2 + 4x#.
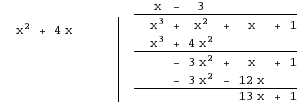
So, we have #(x^3 + x^2 + x + 1)/(x^2 + 4x) = x - 3 + (13x+ 1)/(x^2 + 4x)#
We can integrate #x - 3# using the power rule. However, we will need to use partial fractions for the second part of the integral.
#x^2 + 4x# can be factored as #x(x + 4)#.
#A/x + B/(x + 4) = (13x + 1)/(x(x + 4))#
#A(x + 4) + B(x) = 13x + 1#
#Ax + 4A + Bx = 13x + 1#
#(A + B)x + 4A = 13x + 1#
Write a system of equations:
#{(A + B = 13), (4A = 1):}#
Solving, we get #A = 1/4# and #B = 51/4#.
#=intx - 3 + 1/(4x) + 51/(4(x + 4)) dx#
#= 1/2x^2 - 3x + 1/4ln|x| + 51/4ln|x + 4| + C#
Hopefully this helps!