the #tan# of a negative number is minus the #tan# of its positive value.
this is the same for #tan^-1# of a negative number:
#tan^-1(-theta) = -tan^-1theta#
this means that #tan^-1(-sqrt3) = -tan^-1(sqrt3)#.
#sqrt(3) = tan 60^@#, as can be seen by drawing a triangle:
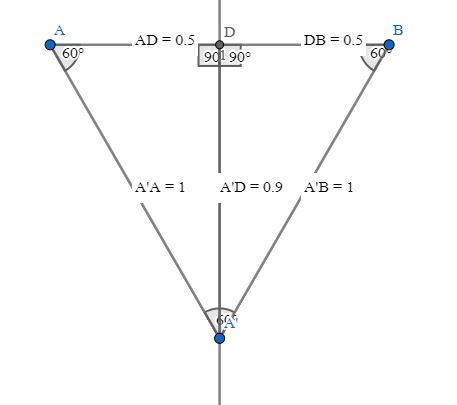
here, an equilateral triangle is drawn and bisected to make two right-angled triangles.
since the outer triangle is equilateral, there is a #60^@# angle.
#tan 60^@# can be found by dividing the length of the side opposite to the angle by the length of the side adjacent to it.
here, the adjacent is #0.5# exactly.
the opposite side, calculated using Pythagoras' Theorem, is #sqrt(1^2-(0.5)^2)#, which is #sqrt(0.75)#.
(in the diagram, it is shown as #0.9#, since this is #sqrt(0.75)# rounded to #1# significant figure.)
#tan 60^@# is #(sqrt0.75)/(0.5)#,
which is #2 * sqrt0.75#.
#2 * sqrt0.75# is the same as #sqrt4 * sqrt0.75#
following the law of surds where #sqrta * sqrtb = sqrtab#,
#sqrt4 * sqrt0.75 = sqrt3#.
therefore, #tan 60^@# must be #sqrt3#.

