Basic Inverse Trigonometric Functions
Key Questions
-
The basic inverse trigonometric functions are used to find the missing angles in right triangles. While the regular trigonometric functions are used to determine the missing sides of right angled triangles, using the following formulae:
#sin theta# = opposite#divide# hypotenuse
#cos theta# = adjacent#divide# hypotenuse
#tan theta# = opposite#divide# adjacentthe inverse trigonometric functions are used to find the missing angles, and can be used in the following way:
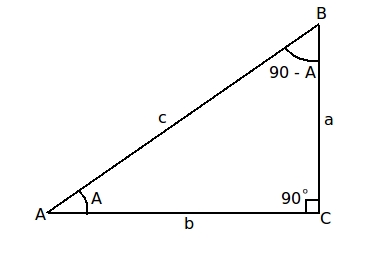
For example, to find angle A, the equation used is:
#cos^-1# = side b#divide# side c -
#sinx=n# if and only if#x=arcsinn + 2 pi k# for some integer#k# or
#x=(pi-arcsinn) + 2 pi k# for some integer#k# #cosx=n# if and only if#x=arccosn + 2 pi k# for some integer#k# or
#x=(pi+arccosn) + 2 pi k# for some integer#k# #tanx=n# if and only if#x=arctan n + pi k# for some integer#k# and so on.
So,: Solve
#7sinx-5 = 0# #7sinx-5 = 0#
#7sinx = 5#
#sinx = 5/7# #x=arcsin(5/7) +2 pi k# for integer#k#
or#(pi-arcsin(5/7)) +2 pi k# for integer#k# -
- Know that arccos, arcsec functions are restricted to quad 1 and 2
- Know that arctan, arccot, arcsin, arccsc are restricted to quad 1 and 4
- And when you go to quadrant 4 with arctan, arccot, arcsin, arccsc, use negative angles
Examples
1.#arcsin(1)= pi/2#
2.#arctan(-1)= -pi/4#
3.#arcsec(1/2)= DNE#
4.#arc csc (-sqrt2)= -pi/4#