What are the Basic Inverse Trigonometric Functions?
1 Answer
Feb 2, 2015
The basic inverse trigonometric functions are used to find the missing angles in right triangles. While the regular trigonometric functions are used to determine the missing sides of right angled triangles, using the following formulae:
the inverse trigonometric functions are used to find the missing angles, and can be used in the following way:
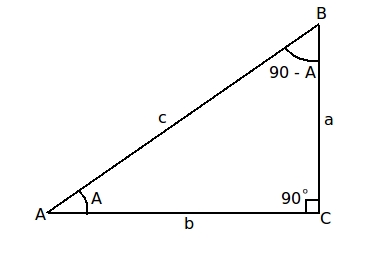
For example, to find angle A, the equation used is:

