Basic formula of binomial theorem,
#(ax+b)^n#
#=(""_0^n)((ax)^n)(b^0)+(""_1^n)((ax)^(n-1))(b^1)+...+(""_r^n)((ax)^(n-r))(b^r)+...+(""_n^n)((ax)^(n-n))(b^n)#
#=(ax)^n+(n)((ax)^(n-1))(b)+...+(""_r^n)((ax)^(n-r))(b^r)+...+(b^n)#
So what is #(""_r^n)#?
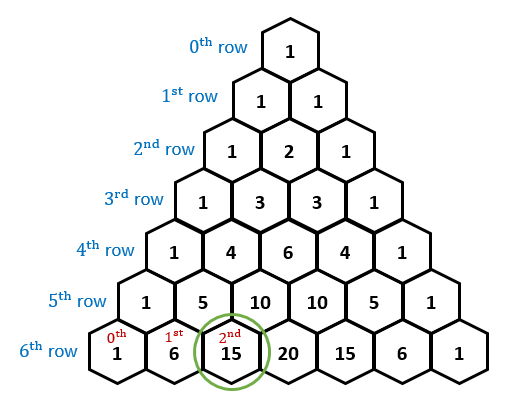
#(""_r^n)#, also known as #""^nC_r#, is a function which lets you deduce a specific number on the Pascal's triangle.
#(""_r^n)=(n!)/((r!)(n-r)!)# ( or you can press your calculator )
Take for example, row #6# and position #2#,
#(""_2^6)=(6!)/((2!)(6-2)!)#
#color(white)(( ""_2^6))=15#
Back to the question, substitute in the #a#, #b# and #n# values,
#(3x+2)^9#
#=(""_0^9)((3x)^9)(2^0)+(""_1^9)((3x)^(9-1))(2^1)+(""_2^9)((3x)^(9-2))(2^2)+(""_3^9)((3x)^(9-3))(2^3)+(""_4^9)((3x)^(9-4))(2^4)+(""_5^9)((3x)^(9-5))(2^5)+(""_6^9)((3x)^(9-6))(2^6)+(""_7^9)((3x)^(9-7))(2^7)+(""_8^9)((3x)^(9-8))(2^8)+(""_9^9)((3x)^(9-9))(2^9)#
#=(1)((3x)^9)(2^0)+(9)((3x)^(8))(2^1)+(36)((3x)^(7))(2^2)+(84)((3x)^(6))(2^3)+(126)((3x)^(5))(2^4)+(126)((3x)^(4))(2^5)+(84)((3x)^(3))(2^6)+(36)((3x)^(2))(2^7)+(9)((3x)^(1))(2^8)+(1)((3x)^(0))(2^9)#
#=(1)(19683x^9)(1)+(9)(6561x^(8))(2)+(36)(2187x^(7))(4)+(84)(729x^(6))(8)+(126)(243x^(5))(16)+(126)(81x^(4))(32)+(84)(27x^(3))(64)+(36)(9x^(2))(128)+(9)((3x)(256)+(1)(512)(1)#
#=19683x^9+118098x^8+314928x^7+489888x^6+489888x^5+326592x^4+145152x^3+41472x^2+6912x+512#
Yeah, it's a tad bit long, I know.

