How do you expand #(3x-5y)^6# using Pascal’s Triangle?
1 Answer
Like this:
Explanation:
Courtesy of Mathsisfun.com 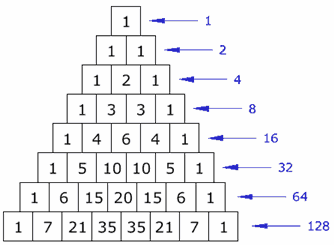
In Pascal's triangle, the expansion which is raised to the power of 6 corresponds to the 7th row of Pascal's triangle. (Row 1 corresponds to an expansion raised to the power of 0, which is equal to 1).
Pascal's triangle denotes the coefficient of every term in the expansion
=
Although, when it comes to any expansion which is above the power of 4 or 5, you are better off using The Binomial Theorem, here explained by Wikipedia.
Use this instead of Pascal's triangle, as it can become very tedious if you have an expansion involving 10+ terms...

