Question

How do you expand `(d-4)^6` using Pascal’s Triangle?

Answer 1

as follws

Explanation:

The power of the given binomial expression `(d-4)^6` is 6

• Generate a Pascal's triangle of 6+1=7 rows as follows
  
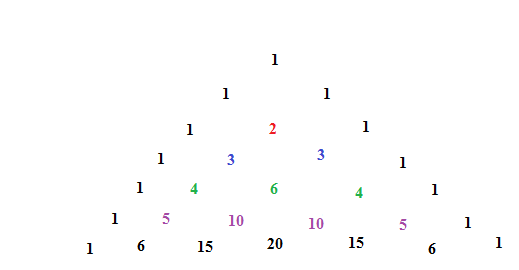
• The numbers of last row i.e (1,6,15,20,15,6,1) are to be taken as coefficients of the terms starting from first one with alternative plus ('+') and minus ( '-') sign as there exist a minus sign between two terms in the given expression.
• The power first term d will decrease by unity from 6 and will end at zero.
• The power of 2nd term 4 will increase by unity from zero and will end at 6

Hence the expansion becomes
`(d-4)^6=1*d^6*4^0-6*d^5*4^1+15*d^4*4^2-20*d^3*4^3 +15*d^2*4^4-6*d^1*4^5+1*d^0*4^6`

`=d^6-24d^5+240d^4-1280d^3+3840d^2-6144d+4096`