Question

How do you expand `(x+2y)^7`?

Answer 1

You should use the binomial theorem. This will give you the answer "quickly". Details below...

Explanation:

The binomial theorem looks like this

`(x+y)^n = sum""_n C_k x^(n-k)y^k`

where the sum runs from k=0 to k= n.

The coefficient for each term in the sum is given by the combination `""_nC_k = (n!)/(k!(n-k)!`

You save a lot of time calculating all these coefficients if you diagram a Pascal's triangle as below:

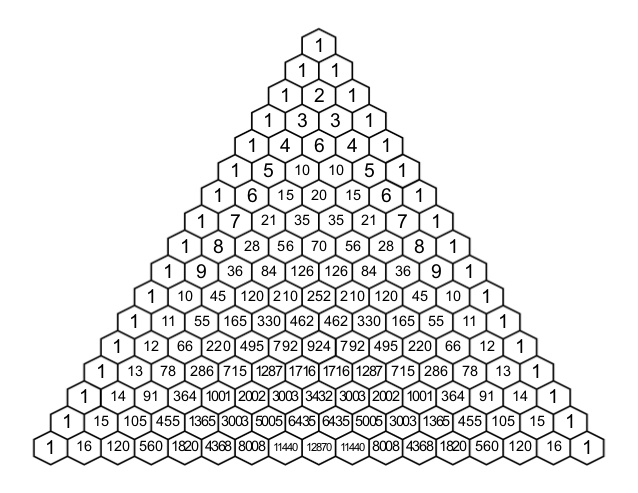
Since the above equation has a "7" as the exponent, look to the row that has a 7 as the second value. These numbers are the coefficients of your expansion!

Now, for the first term, k=0, the second has k=1, and so on. So the expansion becomes

`(x+2y)^7 = 1x^7y^0+7x^6(2y)^1+21x^5(2y)^2+35x^4(2y)^3+35x^3(2y)^4+21x^2(2y)^5+7x^1(2y)^6+1x^0(2y)^7`

Cleaned up a bit, it becomes

`(x+2y)^7 = x^7+14x^6y+84x^5y^2+280x^4y^3+560x^3y^4+672x^2y^5+448x^1y^6+128y^7`

In this final expression, I have combined the coefficients from Pascal's triangle with the integer part of `(2y)^n` (the `2^n` part in other words).