How do you expand # (x + y)^6# using Pascal’s Triangle?
1 Answer
The row of Pascal's triangle starting
Explanation:
Write out Pascal's triangle as far as the row that begins
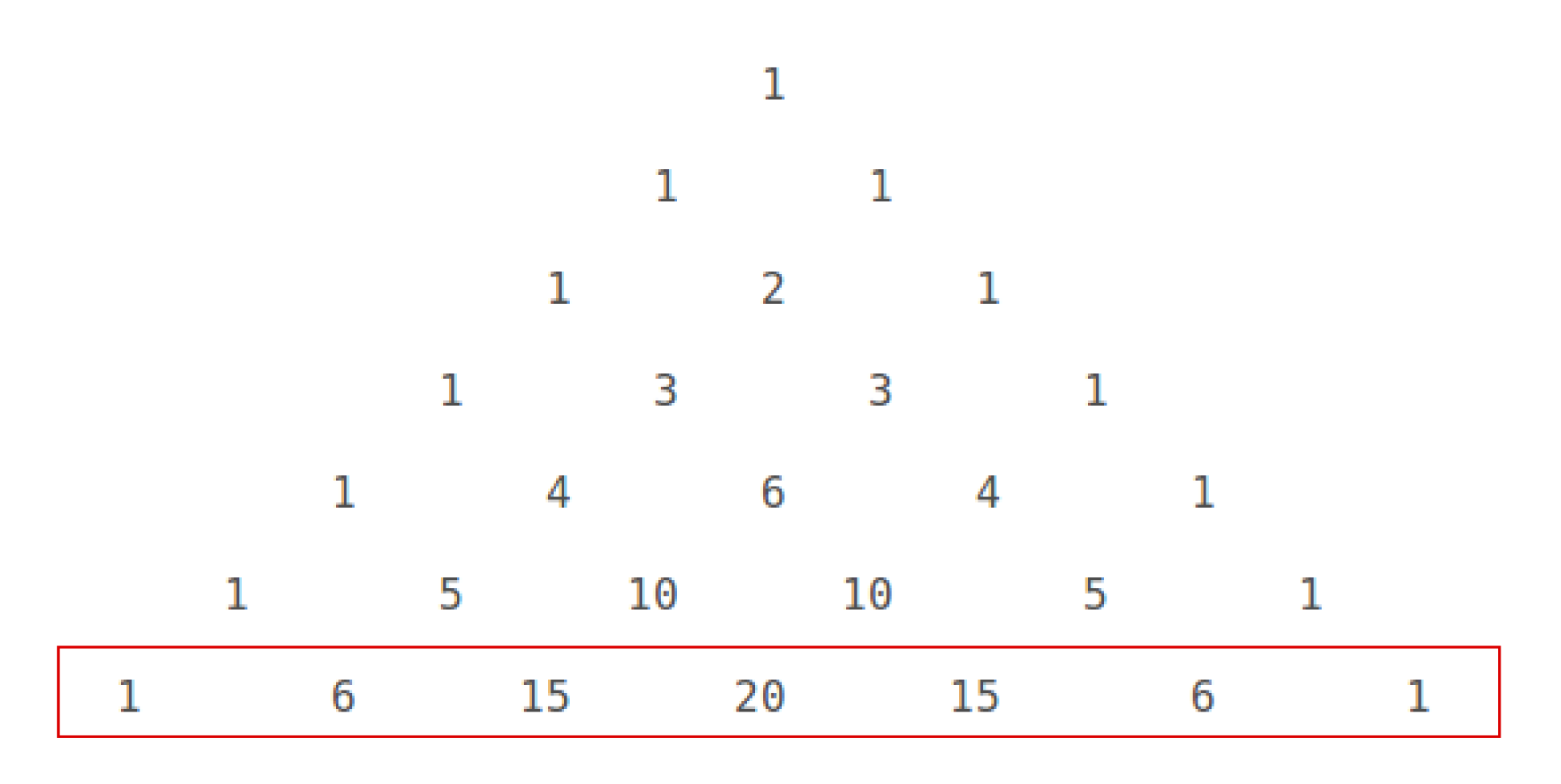
These are the coefficients you need for the expansion:
Why does this work?
If we write out the value as a product of binomials we have:
If you pick one term from each binomial and multiply them together, then you have made
Otherwise, you are making a mixture of left and right choices, analogous to picking your way down from the top of Pascal's triangle to the bottom, via a sequence of left and right branches. The power of
Each number in Pascal's triangle is the sum of the two above, each of which counts the number of ways to reach that point by a sequence of left and right choices. So all of the numbers in Pascal's triangle count the number of ways to reach them by left/right choices starting at the top.

