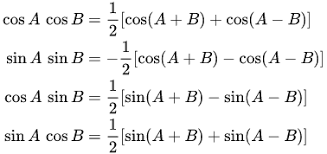How do you express #sin(pi/12) * cos(( 7 pi)/12 ) # without products of trigonometric functions?
2 Answers
Jul 1, 2018
Explanation:
Jul 1, 2018
Explanation: