First of all we have to know that \sin(pi/4)=1/\sqrt(2) and \cos(pi/4)=1/\sqrt(2). We can see this fact considering the diagonal of a square with side of 1. The length of the diagonal, because of the Pitagora's Theorem, is sqrt(1^2+1^2)=sqrt(2). The triangle has one angle of 90^\circ (that is \pi/2 and two of 45^\circ that are \pi/4 as in the image.
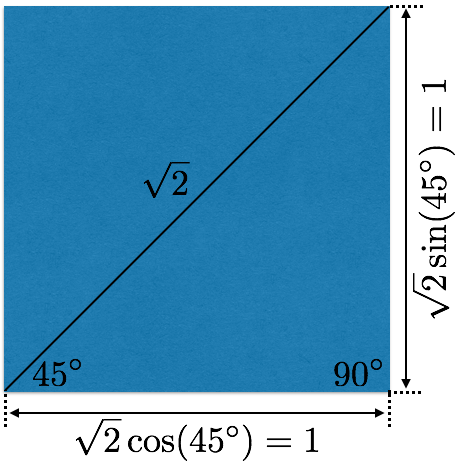
Using the definition of sin and cos it is easy to see that the value of both sin and cos of pi/4 is 1/sqrt(2).
What about the cos(7/4pi)? This is simple if we see what 7/4pi is on a circunference, as in the picture.
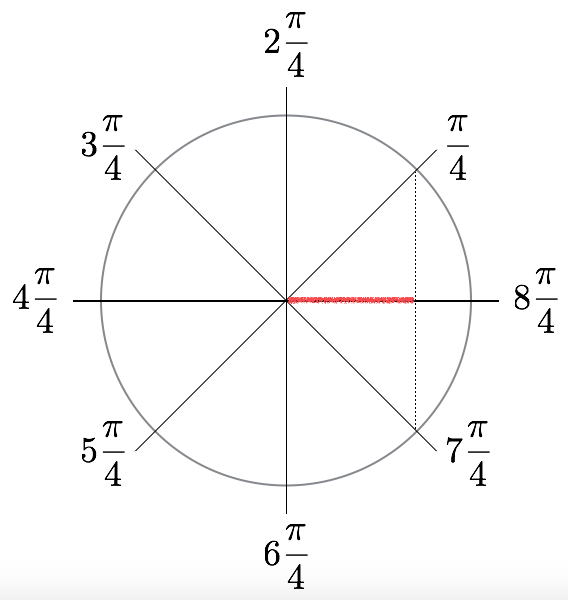
It is clear that 7/4pi is nothing but -pi/4 and the cosine has the property that it stay unchanged if you change the sign of the angle (and from the picture it is simple to see just looking at the cosine as the red line).
Then we have: sin(pi/4)cos(7/4pi)=1/sqrt(2)cos(-pi/4)=1/sqrt(2)cos(pi/4)=1/sqrt(2)1/sqrt(2)=1/2.



