How do you factor the expression 2x^2+7x+1 ?
2 Answers
Mar 30, 2018
the answer is
Explanation:
you can't take out so you have to use the quadratic formula. formula:
Mar 30, 2018
check below
Explanation:
Since you can not use middle-term techniques over here.. So u can use the formula of discriminant:
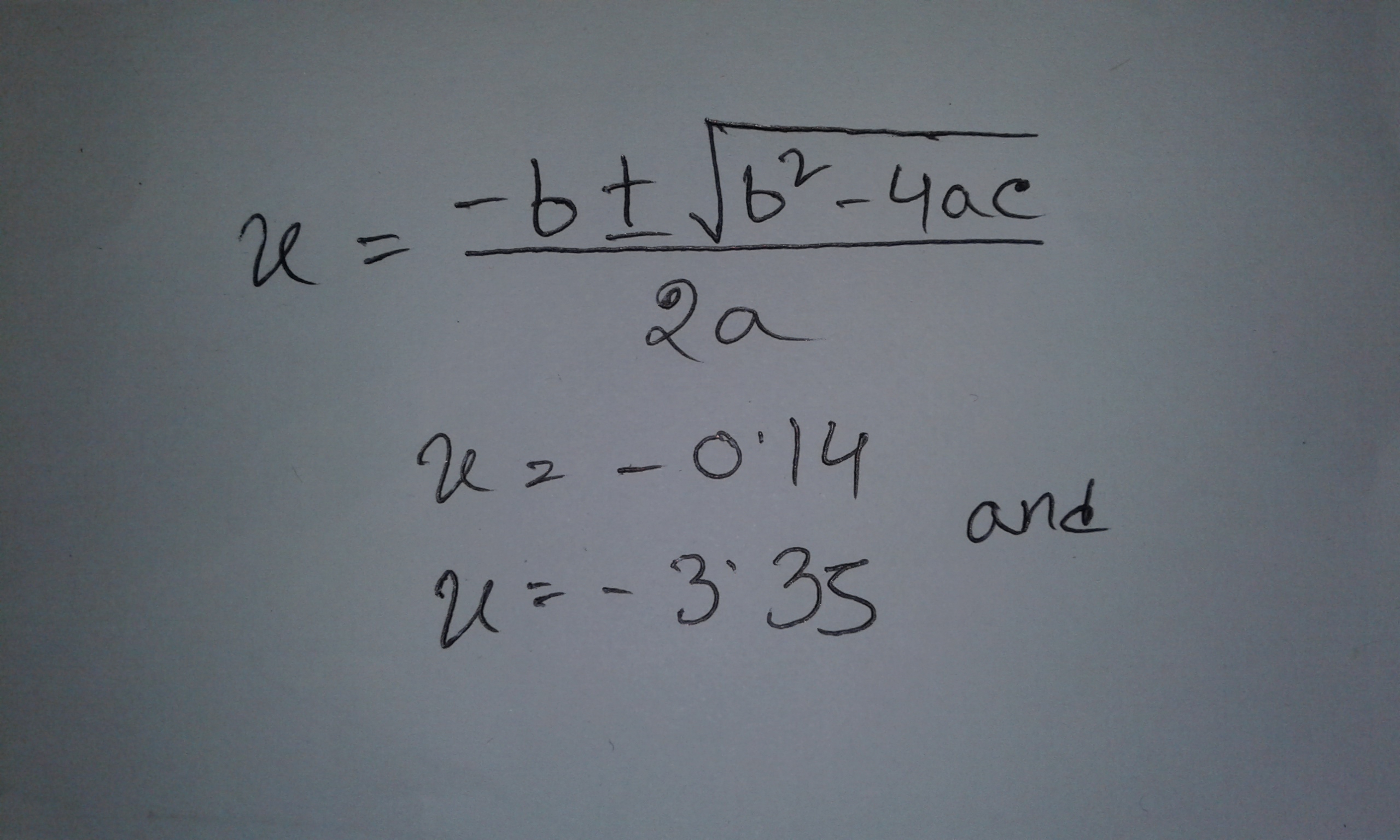 myself
myself
The equation is :
Here a,b,c are the coefficients of


