How do you factor #x^(12) -1#?
2 Answers
Break the problem down to the exponents you can handle. Ideally, Difference of Squares or sum and difference of cubes can be used. An explanation is given below on how to go about it.
Explanation:
Factoring
Let us recollect some rules.
-
Difference of squares
#a^2-b^2 = (a-b)(a+b)# -
Difference of cubes
#a^3-b^3 = (a-b)(a^2+ab+b^2)# -
Sum of cubes
#a^3+b^3 =(a+b)(a^2-ab+b^2)#
Now let us come to our problem.
Let us make x^12 into something which we can recognize easily.
Let us factorize
Now to factorize
Factors of
Rearranging
Use Complex arithmetic, then match up conjugate pairs to find:
#x^12 - 1 =(x-1)(x^2-sqrt(3)x+1)(x^2-x+1)(x^2+1)(x^2+x+1)(x^2+sqrt(3)x+1)(x+1)#
Explanation:
Here's an alternative method using Complex arithmetic to produce a result with Real coefficients...
Note that if
The twelve Complex roots of
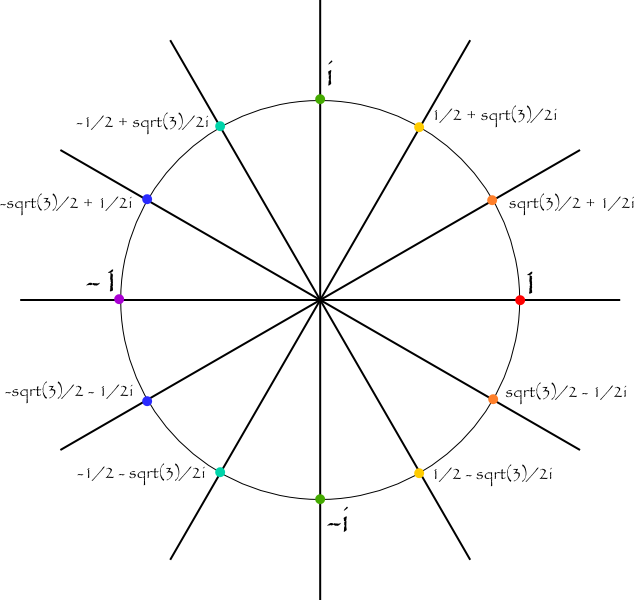
I have marked the Complex conjugate pairs with the same colour.
For example:
So, picking out the roots from right to left, then multiplying up Complex conjugate pairs we find:
#x^12 - 1#
#=(x-1)(x-sqrt(3)/2-1/2i)(x-sqrt(3)/2+1/2i)(x-1/2-sqrt(3)/2i)(x-1/2+sqrt(3)/2i)(x-i)(x+i)(x+1/2-sqrt(3)/2i)(x+1/2+sqrt(3)/2i)(x+sqrt(3)/2-1/2i)(x+sqrt(3)/2+1/2i)(x+1)#
#=(x-1)(x^2-sqrt(3)x+1)(x^2-x+1)(x^2+1)(x^2+x+1)(x^2+sqrt(3)x+1)(x+1)#


