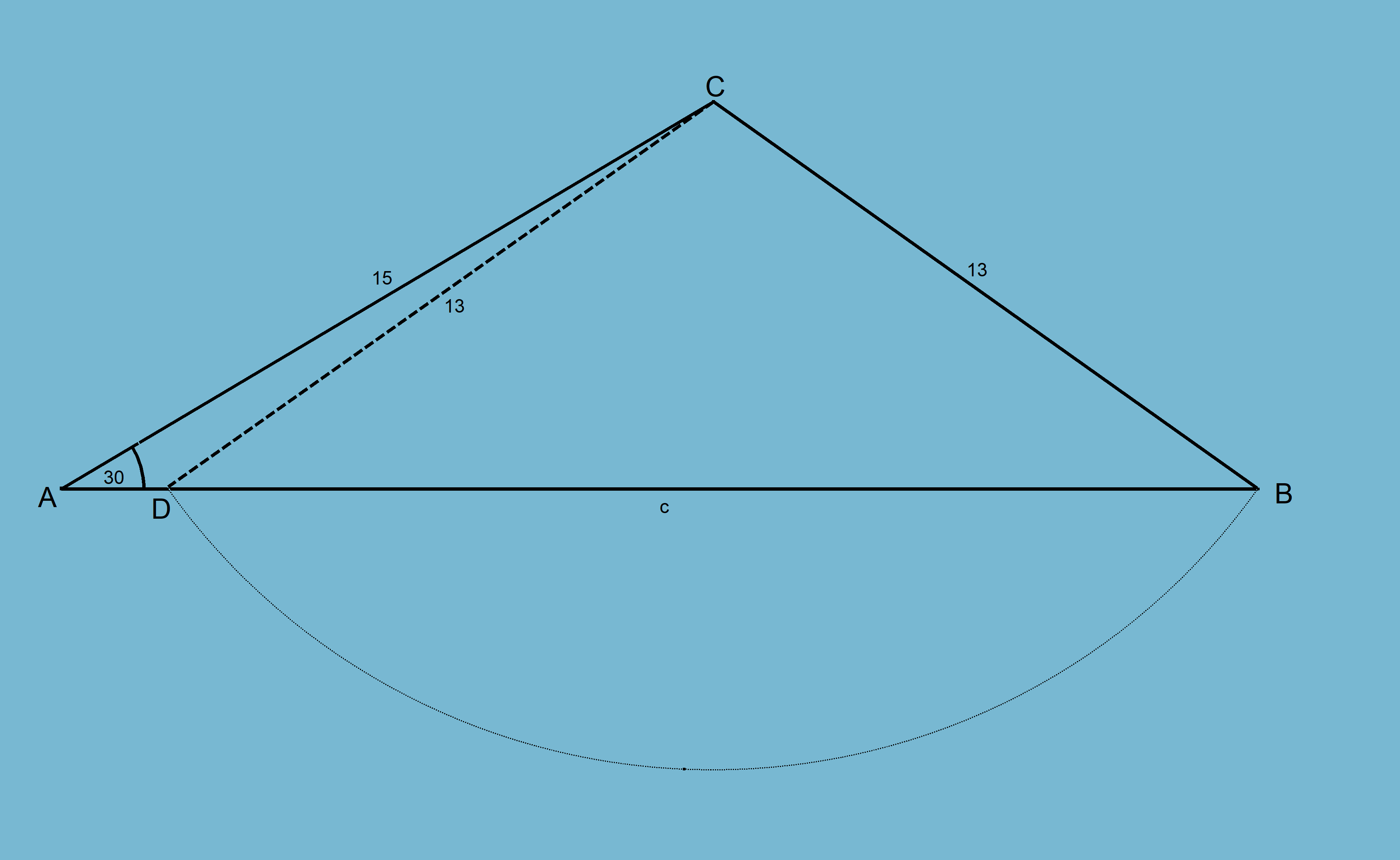
From the diagram you can see that we have an ambiguous case. This gives us to unique triangles:
ABC and ACD
Using the sine rule:
#sinA/a=sinB/b=sinC/c#
Solving for #/_ABC#
#sin(30)/13=sin(B)/15#
Rearranging:
#sin(B)=(15sin(30))/13=((15)(1/2))/13=15/26#
#B=arcsin(15/26)=35.23^@# 2 d.p.
But we also have another angle #/_ADC#
These are angles on a straight line so:
#/_ADC=180^@-arcsin(15/26)=144.77^@# 2 d.p.
Triangle ABC#[1]#
Using #B=35.23^@#
#/_ACB=180^@-(30^@+35.23^@)=114.77^@#
Side #c#:
#sin(30^@)/13=sin(114.77)/c#
#c=(13sin(114.77))/(sin(30^@))=23.61#
So triangle ABC#[1]#
#bbA=30^@#
#bb(B)=35.23^@#
#bbC=114.77^@#
#bba=13#
#bb(b)=15#
#bbc=23.61#
Triangle ABC#[2]#
Using #B=144.77^@#
#/_ACB#
#180^@-(114.77^@+30^@)=5.23^@#
side #c#
#sin(30^@)/13=sin(5.23^@)/c#
#c=(13sin(5.23^@))/(sin(30^@))=2.37#
So triangle ABC#[2]#
#bbA=30^@#
#bb(B)=144.77^@#
#bbC=5.23^@#
#bba=13#
#bb(b)=15#
#bbc=2.37#


