The Law of Sines
Key Questions
-
First of all it is useful to say the notation in a triangle:
Opposite at the side
#a# the angle is called#A# ,
Opposite at the side#b# the angle is called#B# ,
Opposite at the side#c# the angle is called#C# .So, the Sinus Law can be written:
#a/sinA=b/sinB=c/sinC# .This Law is useful in all the cases SSA and NOT in the case SAS, in which the Law of Cosinus has to be used.
E.G.: we know
#a,b,A# , then:#sinB=sinA*b/a# and so#B# is known;#C=180°-A-B# and so#C# is known;#c=sinC/sinB*b# -
The minimum data you need to solve a triangle is 3 between sides or angles, with the only exception of the 3 angles.
The Sines Theorem and the Cosines Theorem are "complementary". If you can use one, you can't use the other one. The Cosines Theorem can only be used in the case of having 2 sides and the angle between them. In ALL the other cases you have to use the sines Theorem. -
Answer:
As detailed below.
Explanation:
Ambiguous case occurs when one uses the law of sines to determine missing measures of a triangle when given two sides and an angle opposite one of those angles (SSA).
In this ambiguous case, three possible situations can occur: 1) no triangle with the given information exists, 2) one such triangle exists, or 3) two distinct triangles may be formed that satisfy the given conditions.
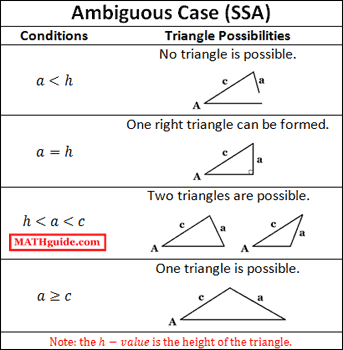
-
Yes, it does. It does not have to be a a right triangle.
I ope that this was helpful.