How do you find all the asymptotes for function #y=(2x^2 + 5x- 3)/(3x+1)#?
2 Answers
See the explanation.
Explanation:
The line
There is no horizontal asymptote, because as
If "all the asymptotes" includes oblique asymptotes, then do the division to get:
So
Vertical Asymptote:
Slant Asymptote:
Explanation:
Vertical Asymptote
To get the vertical asymptote, find the value of
The vertical asymptote is
Horizontal/Slant Asymptote
Since the degree of the numerator is greater than the degree of the denominator by one, we will get a slant asymptote. To solve this, divide
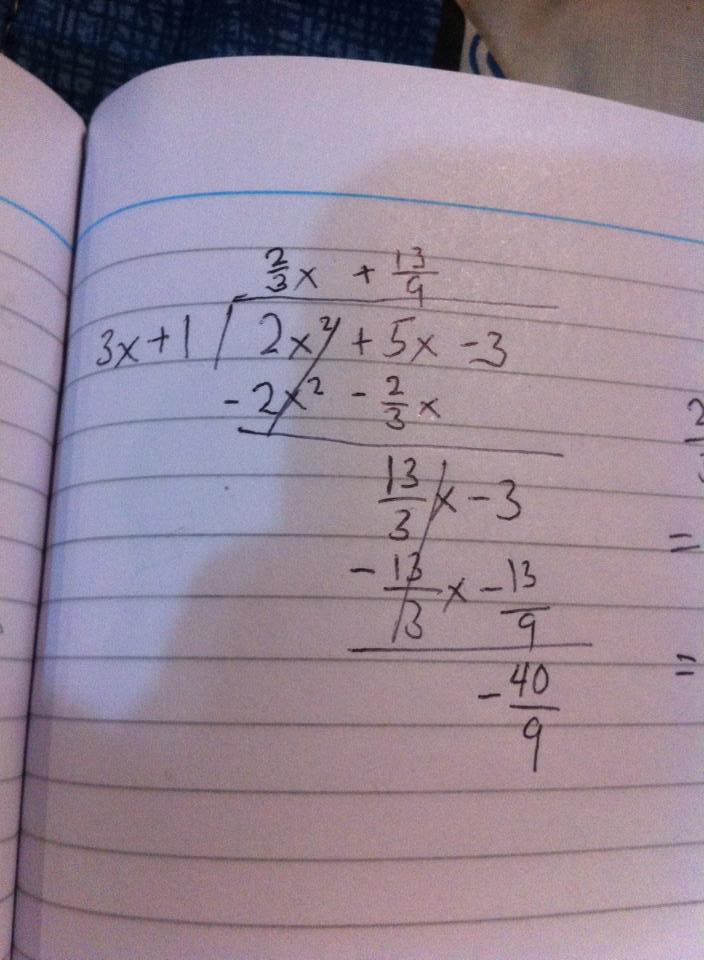 (Sorry for my handwriting)
(Sorry for my handwriting)
Never mind the remainder. The only thing you have to take note of is the polynomial on top.
The slant asymptote is


