How do you find an equation of the parabola with vertex (-2,1) and directrix x=1?

1 Answer
Nallasivam V
Sep 22, 2017

#x=-y^2/6+y/3-13/6#

Explanation:

Given -

Vertex #(-2,1)#
Directrix #x=1#

The vertex is in the 2nd quadrant. The directrix is parallel to the y-axis. So, the parabola opens to the left. The vertex of the parabola is not the origin. Then its general form is -

#(y-k)^2=-4.a.(x-h)#

Where -
#h# and #k# are the coordinates of the vertex.

#h=-2)#

#k=1#

#a=1.5# half the distance between Directrix and vertex [= distance between focus and vertex]

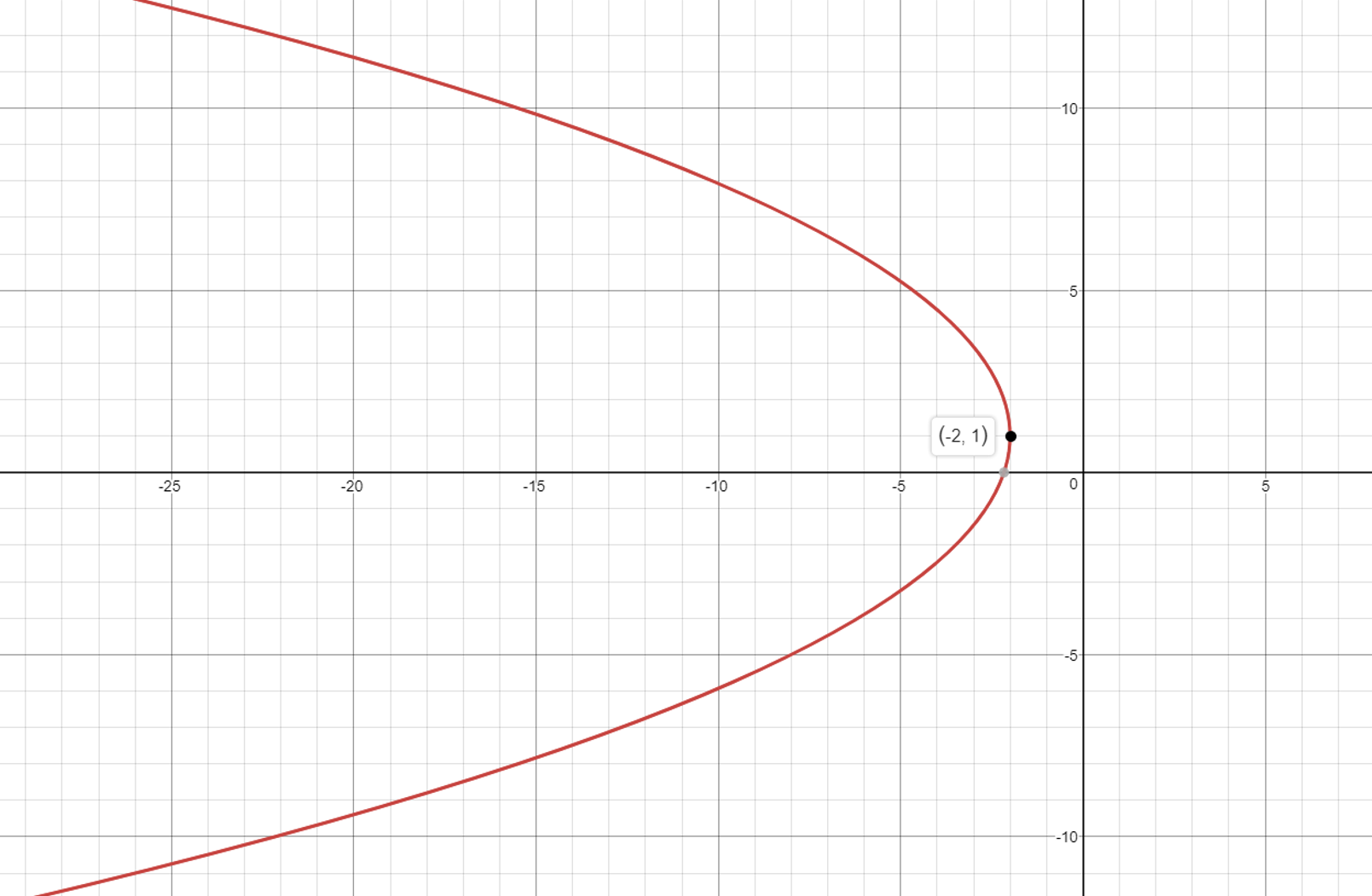
enter image source here

Substitute these values in the equation

#(y-1)^2=-4.1.5.(x+2)#
#y^2-2y+1=-6x-12#
#-6x-12=y^2-2y+1#
#-6x=y^2-2y+1+12#
#x=y^2/(-6)-(2y)/(-6)+13/(-6)#

#x=-y^2/6+y/3-13/6#

Related questions
See all questions in Vertex Form of the Equation
Impact of this question
56433 views around the world
You can reuse this answer
Creative Commons License