How do you find the amplitude and period of a function #y=-3sec(-6x)+2#?

Question

2571 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-13T22:02:10

No amplitude for #secx#, period=#(pi)/3#

Our function is in the form #asec(bx-c)+d#. Look at the graph of #secx# below. What do you notice?:

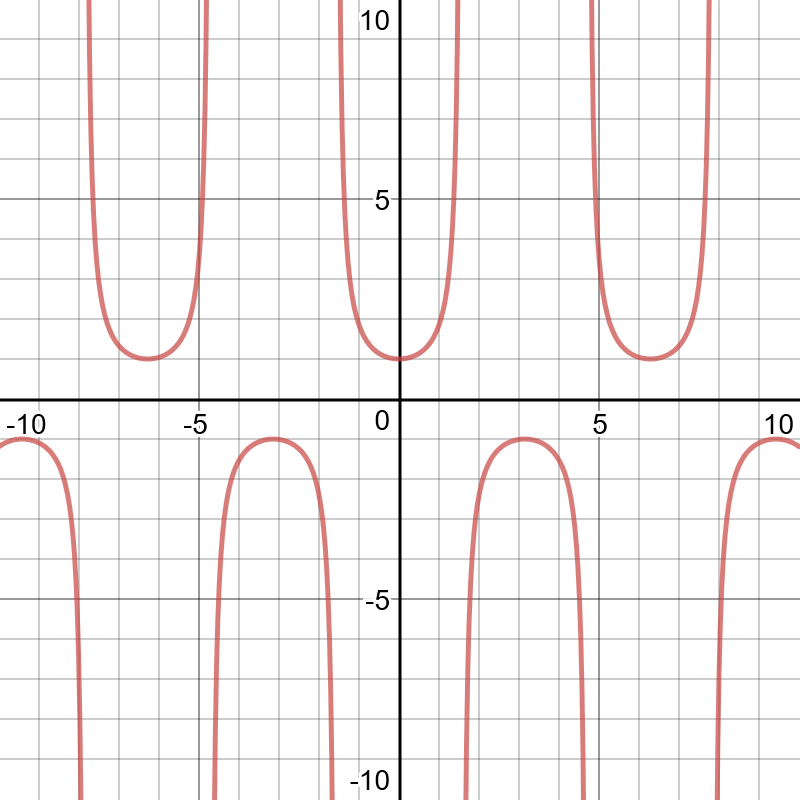
Technically, the graph of #secx# has no maximum or minimum value, therefore there is no amplitude.

The period, however, can be determined using our formula:

#(2pi)/|b|#

In this case, b is the coefficient on our x-term, which is #-6#. We have to take the absolute value of it, which will make it a positive #6#.

#(2pi)/6#, which can be simplified to #(pi)/3#

Additionally, you can find more info on amplitude, period and phase shift on the site below:
https://www.mathway.com/popular-problems/Precalculus/401080