Amplitude, Period and Frequency
Key Questions
-
Frequency and period are related inversely. A period
PP is related to the frequencyf
P = 1/f Something that repeats once per second has a period of 1 s. It also have a frequency of
1/s . One cycle per second is given a special name Hertz (Hz). You may also say that it has a frequency of 1 Hz.A sin function repeats regularly. Its frequency (and period) can be determined when written in this form:
y(t) = sin(2pi f t) -
Answer:
color(red)("Period " = 1 / " Frequency " or " T = 1 / f Explanation:
Frequency is the number of occurrences of a repeating event per unit of time.
It is also referred to as temporal frequency, which emphasizes the contrast to spatial frequency and angular frequency.
The period is the duration of time of one cycle in a repeating event, so the period is the reciprocal of the frequency.
Relationship between Period and frequency is as under :
The frequency of a wave describes the number of complete cycles which are completed during a given period of time.
As such, frequency is a rate quantity which describes the rate of oscillations or vibrations or cycles or waves on a per second basis.
A common unit of frequency is the Hertz, abbreviated as Hz.
color(red)("Frequency " = 1 / " Period" f = c / λ = wave speed c (m/s) / wavelength λ (m).
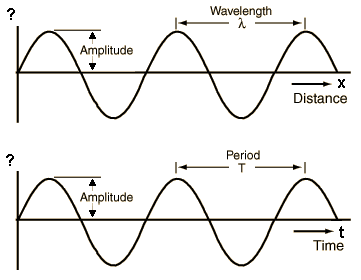

-
"(Amplitude)"=1/2["(Highest Value)"-"(Lowest Value)"]
graph{4sinx [-11.25, 11.25, -5.62, 5.625]}
In this sine wave the highest value is
4 and the lowest is-4 So the maximum deflection from the middle is
4 k.This is called the amplitude
If the middle value is different from
0 then the story still holds
graph{2+4sinx [-16.02, 16.01, -8, 8.01]}You see the highest value is 6 and the lowest is -2,
The amplitude is still1/2 (6- -2)=1/2 *8=4 -
If
f(x)=asin(bx) org(x)=acos(bx) , then their amplitudes are|a| , and the periods are{2pi}/|b| .
I hope that this was helpful.