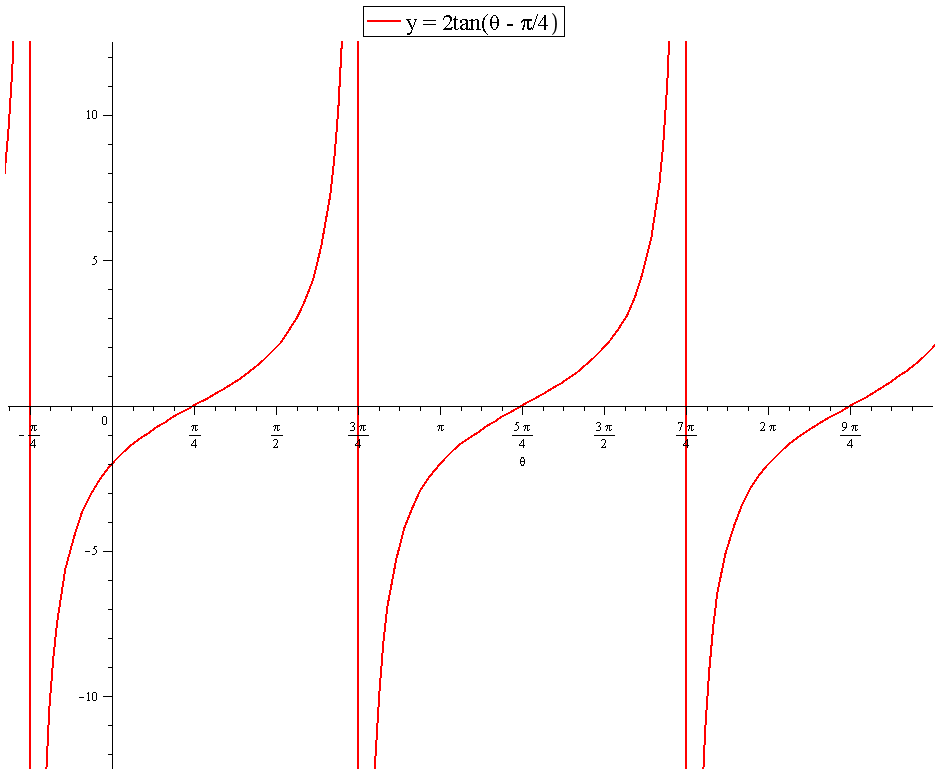
How do you find the amplitude, period, asymptotes (from 0-2pi), shifts, and the min/max of the following trig functions #Y= 2tan ( theta - pi/4)#?
1 Answer
See below.
Explanation:
The tan function has no max/min value and consequently no amplitude. This is because:
as
The shift is
Vertical asymptotes will occur where the function is undefined. This can be calculated using:
Period.
This can be found from two values where the tangent is zero. i.e.
So:
Amplitude Doesn’t exist due to being undefined.
Period
max/min Doesn’t exist due to being undefined.
shift
Asymptotes At
Graph: