Question

How do you find the angle between the vectors `u=<3, 2>` and `v=<4, 0>`?

Answer 1

The angle is `33.7 °`(3sf)

Explanation:

The angle `theta` between two vectors `vec A` and `vec B` is related to the modulus (or magnitude) and scaler (or dot) product of `vec A` and `vec B` by the relationship:

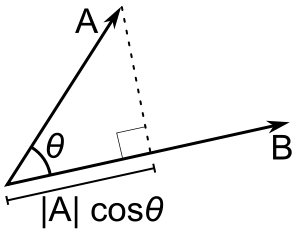
`vec A * vec B = |A| |B| cos theta`

By convention when we refer to the angle between vectors we choose the acute angle.

So for this problem, let the angle betwen `vecu` and `vecv` be `theta` then:

`vec u=<<3, 2>>` and `vec v=<<4, 0>>`

The modulus is given by;

`|vec u| = |<<3, 2>>| = sqrt(3^2+2^2)=sqrt(9+4)=sqrt(13)`
`|vec v| = |<<4, 0>>| = sqrt(4^2+0^2)=sqrt(16)=4`

And the scaler product is:

`vec u * vec v = <<3, 2>> * <<4, 0>>`
`\ \ \ \ \ \ \ \ \ \ = (3)(4) + (2)(0)`
`\ \ \ \ \ \ \ \ \ \ = (12)`

And so using `vec A * vec B = |A| |B| cos theta` we have:

`12 = sqrt(13) * 4 * cos theta`
`:. cos theta = (12)/(4sqrt(13))`
`:. cos theta = 0.83205 ...`
`:. theta = 33.69006 °`
`:. theta = 33.7 °`(3sf)