Question

How do you find the angle between the vectors `u=6i+3j` and `v=-4i+4j`?

Answer 1

`72°`(3sf)

Explanation:

The angle `theta` between two vectors `vec A` and `vec B` is related to the modulus (or magnitude) and scaler (or dot) product of `vec A` and `vec A` by the relationship:

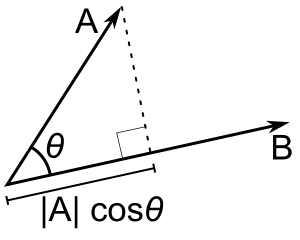
`vec A * vec B = |A| |B| cos theta`

By convention when we refer to the angle between vectors we choose the acute angle.

So for this problem, let the angle betwen `vecu` and `vecv` be `theta` then:

`vec u=6 ulhati+3ulhatj=((6),(3))` and `vec v=-4ulhati+4ulhatj=((-4),(4))`

The modulus is given by;

`|vec u| = |((6),(3))| \ \ \ = sqrt(6^2+3^2)=sqrt(36+9)=sqrt(45)=3sqrt(5)`
`|vec v| = |((-4),(4))| = sqrt(-4^2+4^2)=sqrt(16+16)=sqrt(32)=4sqrt(2)`

And the scaler product is:

`vec u * vec v = ((6),(3)) * ((-4),(4))`
`\ \ \ \ \ \ \ \ \ \ = (6)(-4) + (3)(4)`
`\ \ \ \ \ \ \ \ \ \ = -24+12`
`\ \ \ \ \ \ \ \ \ \ = -12`

And so using `vec A * vec B = |A| |B| cos theta` we have:

`-12 = 3sqrt(5) * 4sqrt(2) * cos theta`
`:. cos theta = (-12)/(12sqrt(5) sqrt(2))`
`:. cos theta = -0.316227 ...`
`:. theta = 108.4349 °`
`:. theta = 108 °`(3sf)

So the acute angle between the vectors is `72°`(3sf)