How do you find the area between #f(x)=10/x, x=0, y=2, y=10#?
2 Answers
Area
Explanation:
First examine the area drawn on a graph:
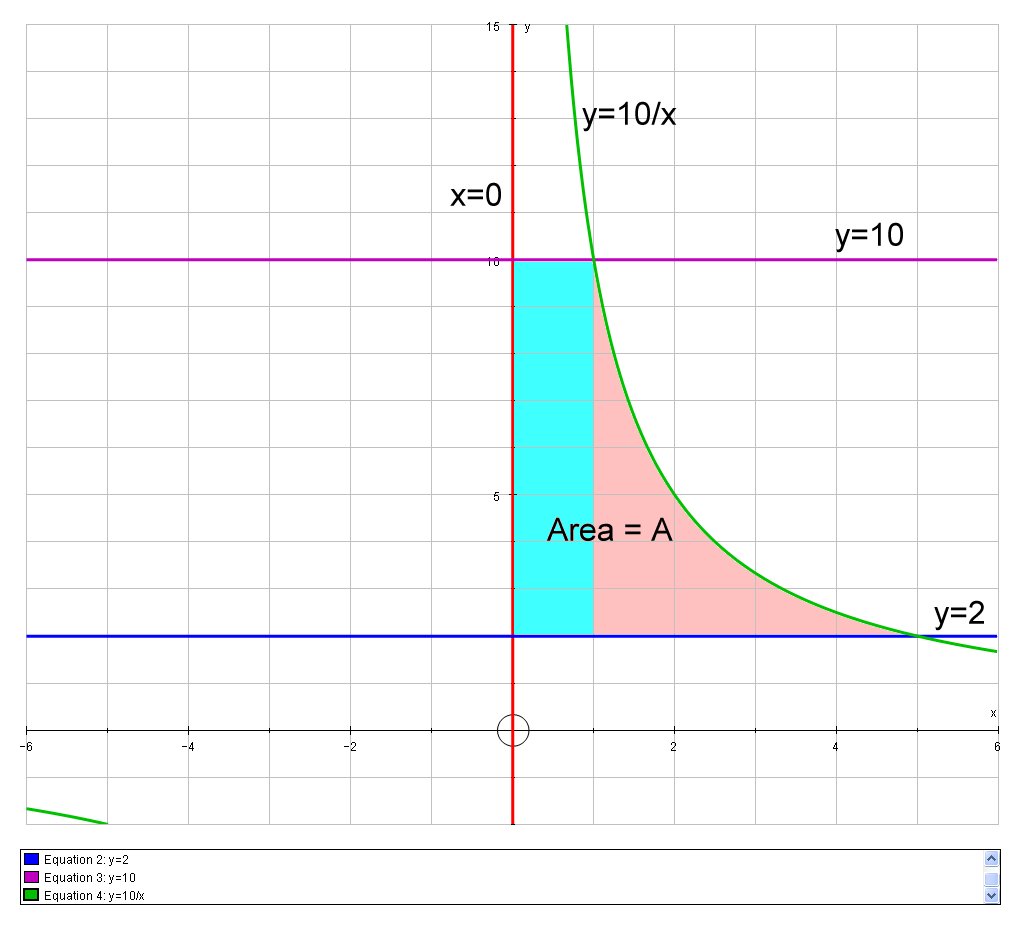
The bounded area,
# A_1 = 1 xx 8 = 8 #
And the remaining Area, is that under the curve
#10/x=2 => x=5# , and#10/x=10=>x=1#
This area is then given by:
# A_2 = int_1^5 (10/x-2) \ dx #
# \ \ \ \ \= [10lnx-2x color(white)int]_1^5#
# \ \ \ \ \= (10ln5-10) - (10ln1-2)#
# \ \ \ \ \= 10ln5-10 - 0 + 2#
# \ \ \ \ \= 10ln5-8#
And so the total bounded area is:
#A= A_1+ A_2#
#\ \ \ = 8+10ln5-8#
#\ \ \ = 10ln5#
Explanation:
graph{x(y-2)(y-10)(xy-10)=0 [-20, 20, -10, 10]}
The curved boundary is the branch of the rectangular hyperbola
xy = 10, in
The area is

