Here is a graph of the two functions, #f(x)=root3(x-1), g(x)=x-1#:
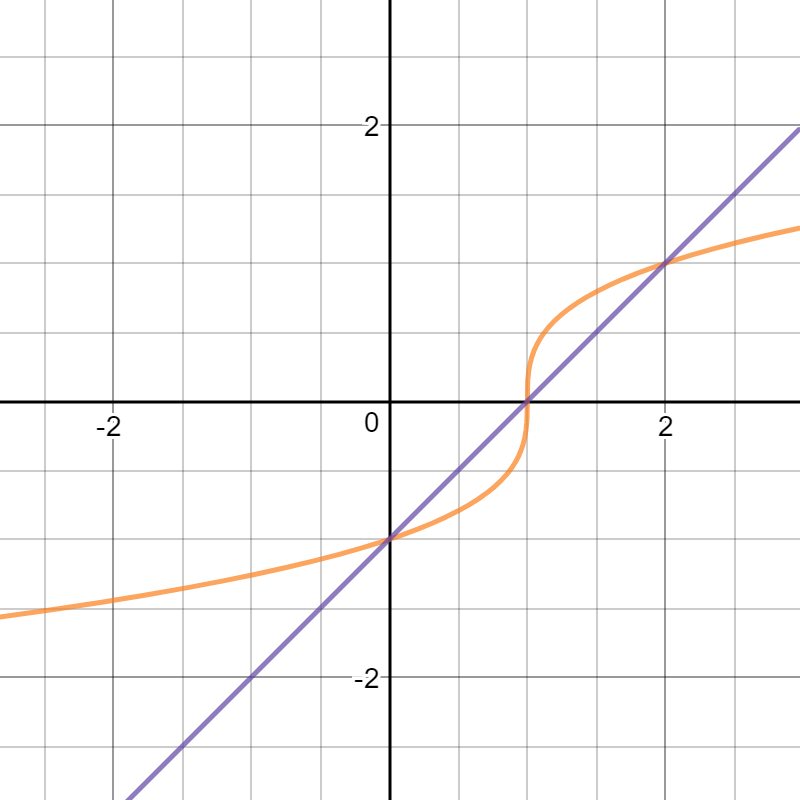
Please observe that from #x =0# to #x = 1#, #g(x) > f(x)#, therefore, the integral is:
#A = int_0^1 g(x)-f(x)dx#
From #x =1# to #x =2# #f(x)>g(x)#, therefore, we subtract #g(x)# from #f(x) in this region:
#A = int_0^1 g(x)-f(x)dx+ int_1^2 f(x)-g(x)dx#
Substitute for #f(x) and g(x)#:
#A = int_0^1 x-1 -root3(x-1)dx+ int_1^2 root3(x-1)-x+1dx#
#A = (x^2/2-x -3/4(x-1)^(4/3)]_0^1+ int_1^2 root3(x-1)-x+1dx#
#A = (1^2/2-1 -3/4(1-1)^(4/3))-(0^2/2-0 -3/4(0-1)^(4/3)) + int_1^2 root3(x-1)-x+1dx#
#A = -1/2+3/4 + int_1^2 root3(x-1)-x+1dx#
#A = 1/4 + int_1^2 root3(x-1)-x+1dx#
#A = 1/4 + (3/4(x-1)^(4/3)-x^2/2+x]_1^2#
#A = 1/4 + (3/4(2-1)^(4/3)-2^2/2+2)- (3/4(1-1)^(4/3)-1^2/2+1)#
#A = 1/4 + 3/4-1/2#
#A = 1/2#

