How do you find the area between #f(x)=-x^2+4x+1, g(x)=x+1#?

Question

4428 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-29T19:38:43

Please see the explanation.

Find the boundaries of the area by setting #f(x) = g(x)#

#-x^2 + 4x + 1 = x + 1#

#-x^2 + 3x = 0#

#x = 0 and x = 3#

This is confirmed by the graph of the two functions:

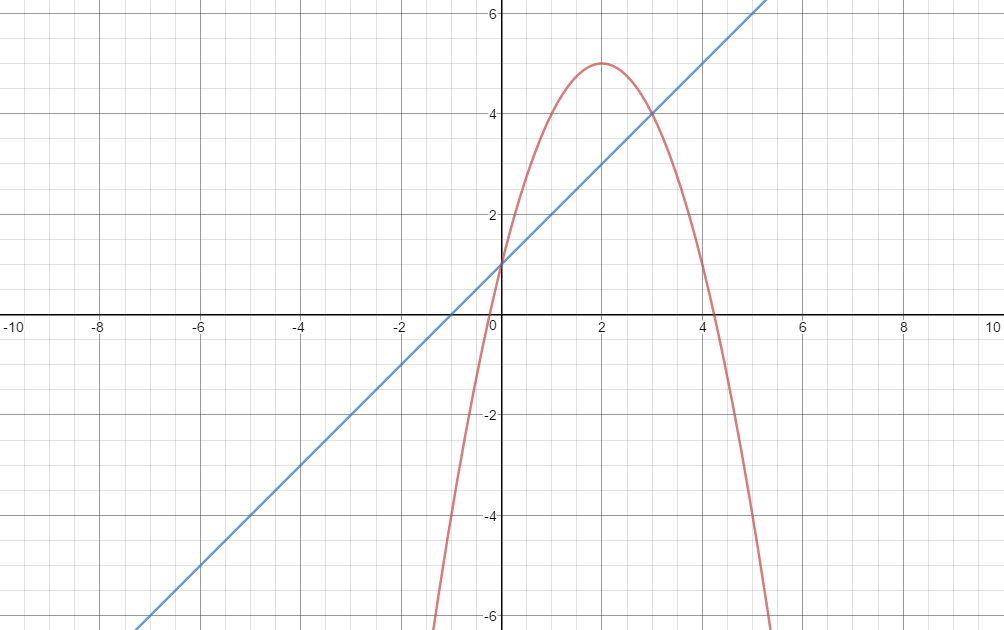
Desmos.com

Let the lower limit of integration# = 0#
Let the upper limit of integration# = 3#

The area between the two fuctions is:

#int_0^3 f(x)dx - int_0^3 g(x)dx =#

#int_0^3 (-x^2 + 4x + 1)dx - int_0^3 (x + 1)dx =#

#int_0^3 (-x^2 + 4x + 1) - (x + 1)dx =#

#int_0^3 (-x^2 + 3x)dx = (-x^3/3 + (3x^2)/2)|_0^3 = 4.5#