How do you find the area between the curves #x+3y=21# and #x+7=y^2#?
1 Answer
Mar 29, 2015
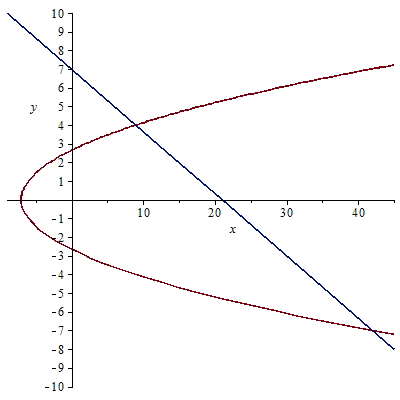
Solve each function for
Now find out where the two curves intersect.
The integral for the area is
Integrating we get
Now evaluate

