Here is a picture of the region whose area we seek.
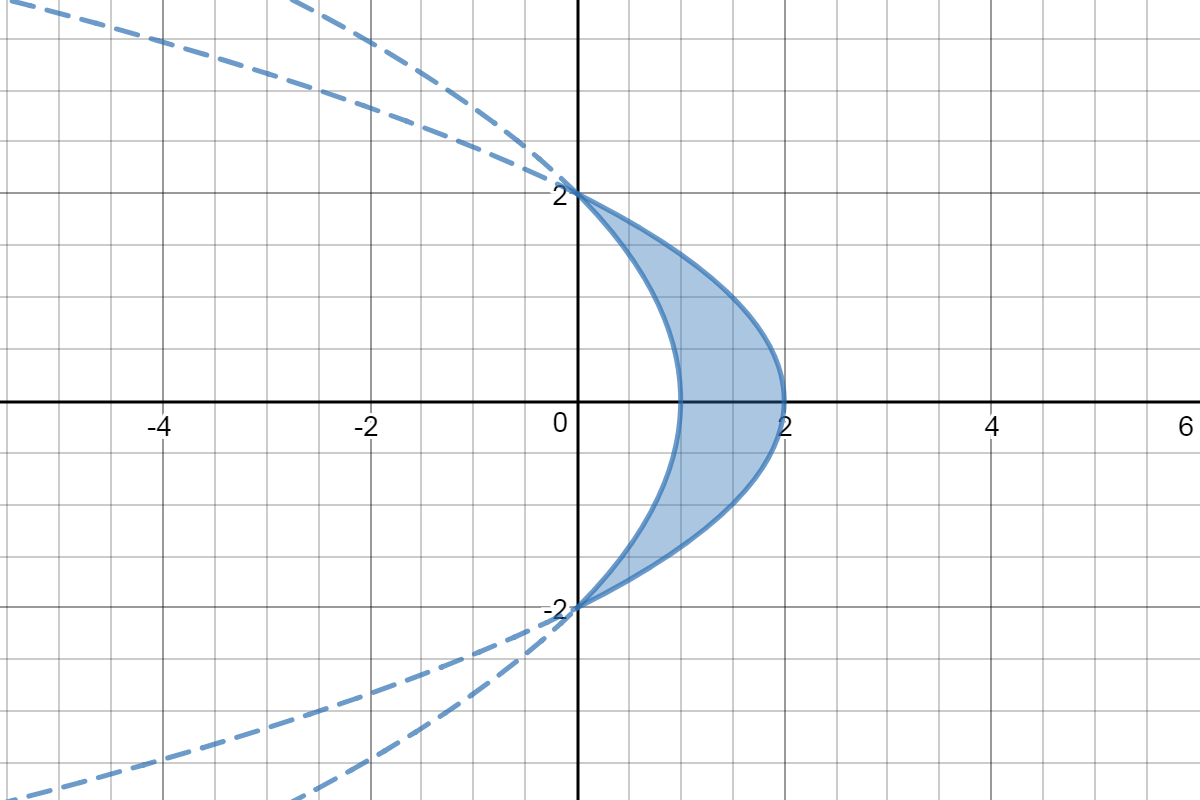
When we first learn to find areas by integration, we take representative rectangles vertically.
The rectangles have base #dx# (a small change in #x#) and heights equal to the greater #y# (the one on upper curve) minus the lesser #y# value (the one on the lower curve). We then integrate from the smallest #x# value to the greatest #x# value.
That approach is quite challenging in this problem.
Here it is very valuable to learn to reflect our thinking #90^@#.
We will take representative rectangles horiontally.
The rectangles have height #dy# (a small change in #y#) and bases equal to the greater #x# (the one on rightmost curve) minus the lesser #x# value (the one on the leftmost curve). We then integrate from the smallest #y# value to the greatest #y# value.
Notice the duality
#{:("vertical ", iff ," horizontal"),
(dx, iff, dy),
("upper", iff, "rightmost"),
("lower", iff, "leftmost"),
(x, iff, y):}#
The phrase "from the smallest #x# value to the greatest #x# value." indicates that we integrate left to right. (In the direction of increasing #x# values.)
The phrase "from the smallest #y# value to the greatest #y# value." indicates that we integrate bottom to top. (In the direction of increasing #y# values.)
Here is a picture of the region with a small rectangle indicated:
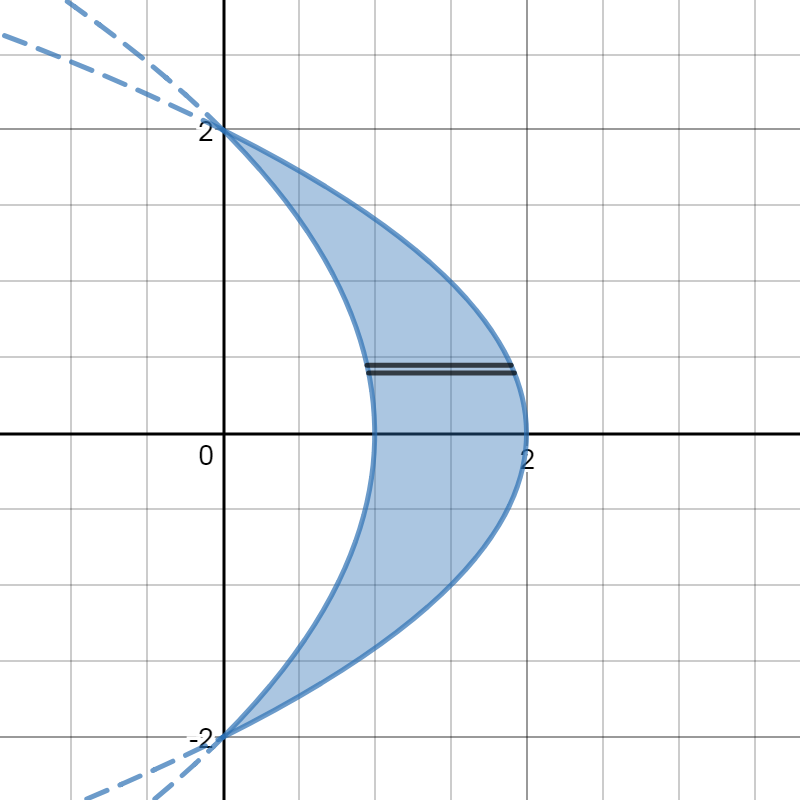
The #x# on the right (the greater #x# value) lies on the graph of #y^2=-2(x-2)#.
Solving for #x#, we get #x_"right" = -y^2/2+2#
The #x# on the left (the lesser #x# value) lies on the graph of #y^2=-4(x-1)#.
Solving for #x#, we get #x_"left" = -y^2/4+1#
#y# varies from #-2# to #2#, so the area of the region is
#int_-2^2 ((-y^2/2+2)-(-y^2/4+1)) dy#
# = int_-2^2 (1-y^2/4) dy = 8/3#



