How do you find the area between y=-3/8x(x-8), y=10-1/2x, x=2, x=8?
2 Answers
Show below
Explanation:
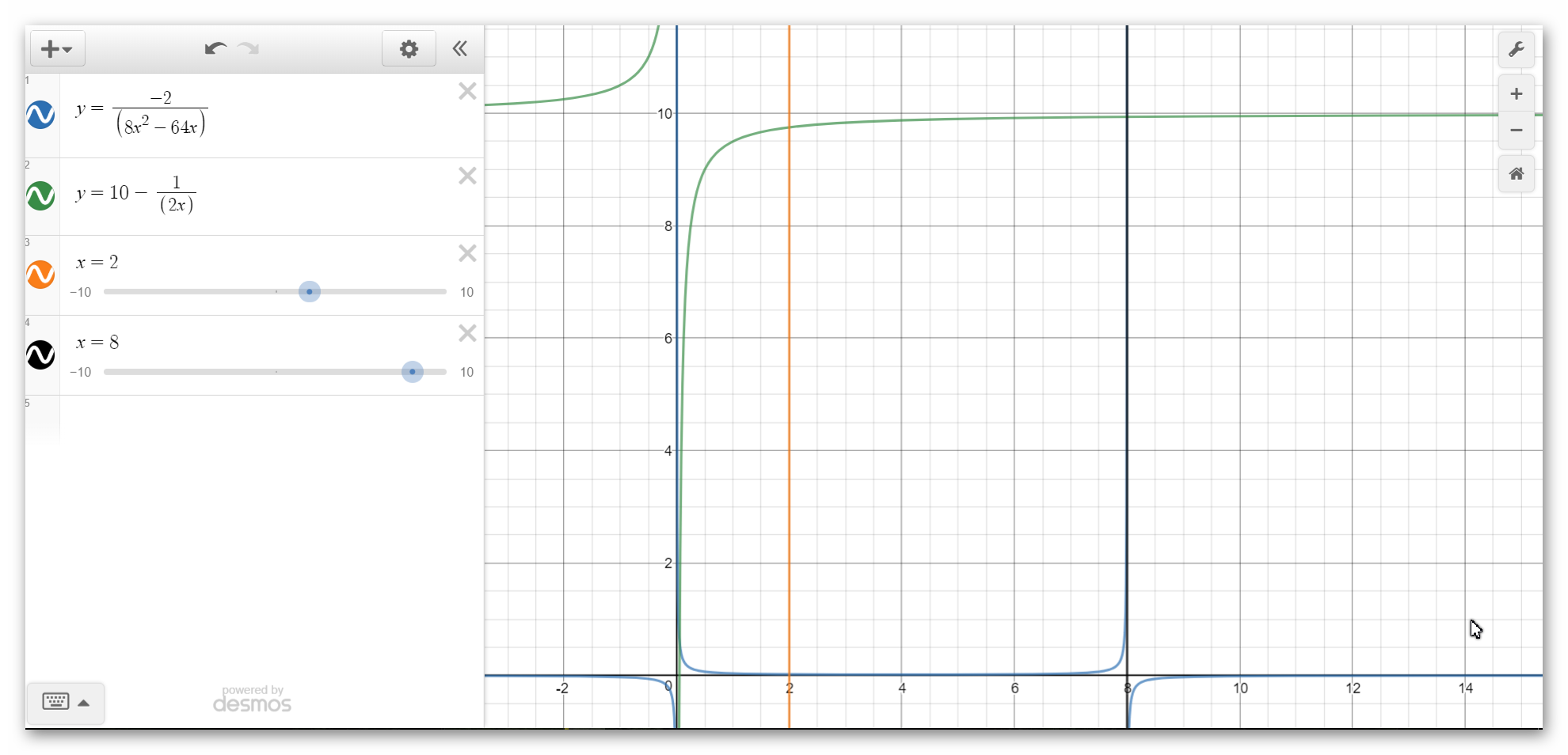
this is a sketch for your functions you can use this website to sketch them[www.desmos.com]
the area between the two curve equal
then complete the steps normally
Explanation:
This is an
So the area enclosed by all four graphs is the area of the trapezium less the area under the curve.
45 - 27 = 18


